
【题目】如图,点A,B的坐标分别为(0,8),(10,0),动点C,D分别在OA,OB上且CD=8,以CD为直径作⊙P交AB于点E,F.动点C从点O向终点A的运动过程中,线段EF长的变化情况为( )
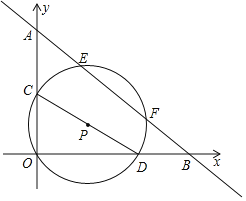
A.一直不变B.一直变大
C.先变小再变大D.先变大再变小
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
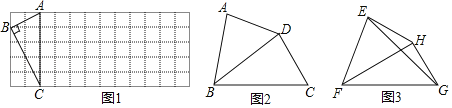
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹);
(2)如图2,在四边形ABCD中,∠ABC=70°,∠ADC=145°,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
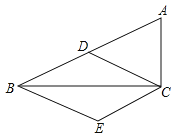
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,过点B、点C分别作BE∥CD,CE∥BD.
(1)求证:四边形BECD是菱形;
(2)若∠A=60°,AC=![]() ,求菱形BECD的面积.
,求菱形BECD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
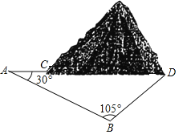
【题目】2019年11月26日,鲁南高铁正式开通运营.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿AC方向挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D共线)处同时施工.测得∠CAB=30°, ,∠ABD=105°,求AD的长.
,∠ABD=105°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小马和小聪想用所学的数学知识测量图书馆前小河的宽,测量时,他们选择河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.35m,BD=7m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
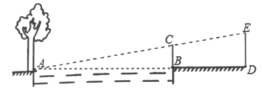
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣2x2+bx+c的图象经过点(0,6)和(1,8).
(1)求这个二次函数的解析式;
(2)①当x在什么范围内时,y随x的增大而增大?
②当x在什么范围内时,y>0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:如图①,若点D在△ABC的边AB上,且满足∠ACD=∠B(或∠BCD=∠A),则称满足这样条件的点为△ABC边AB上的“理想点”.
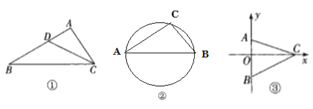
(1)如图①,若点D是△ABC的边AB的中点,AC=![]() ,AB=4.试判断点D是不是△ABC边AB上的“理想点”,并说明理由.
,AB=4.试判断点D是不是△ABC边AB上的“理想点”,并说明理由.
(2)如图②,在⊙O中,AB为直径,且AB=5,AC=4.若点D是△ABC边AB上的“理想点”,求CD的长.
(3)如图③,已知平面直角坐标系中,点A(0,2),B(0,-3),C为x轴正半轴上一点,且满足∠ACB=45°,在y轴上是否存在一点D,使点A是B,C,D三点围成的三角形的“理想点”,若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a<0<b)的图像与x轴只有一个交点,下列结论:①x<0时,y随x增大而增大;②a+b+c<0;③关于x的方程ax2+bx+c+2=0有两个不相等的实数根.其中所有正确结论的序号是( )
A.①②B.②③C.①③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com