
【题目】等边三角形ABC内接于⊙O,连接OA,OB,OC,延长AO分别交BC于点P,弧BC于点D,连接BD,CD.
(1)判断四边形BDCO是哪一种特殊四边形,并说明理由;
(2)若等边三角形ABC的边长6![]() cm,求⊙O的半径;
cm,求⊙O的半径;
(3)在劣弧BD上有一点Q,请求出弓形BQD的面积.
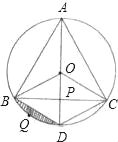
【答案】(1)四边形BDCO是菱形理由见解析;(2)6;(3)6π-9![]() .
.
【解析】
(1)可先由四边形各角的大小求出各边之间的关系,然后即可判断四边形BDCO为何种特殊四边形;
(2)先由菱形性质求出BP的长,再由等边三角形性质及求出∠POB的角度,然后即可由三角形边角关系求出OB的长,即⊙O的半径;
(3)弓形BQD的面积可由求扇形OBD与三角形OBD之差间接求得.
解:(1)四边形BDCO是菱形,理由如下:
∵AB=BC=AC,
∴∠AOB=∠BOC=∠COA=120°,
∴∠BOD=180°﹣∠AOB=60°,
∴∠COD=180°﹣∠AOC=60°;
又∵OB=OD,
∴△OBD为正三角形,
∴OB=OD=BD
同理可得OC=CD,
∴OB=OC=BO=CD即四边形BDCO是菱形;
(2)由菱形性质可知,BP=![]() BC=
BC=![]() ×6
×6![]() =3
=3![]() ;
;
∵△ABC为等边三角形,∠PBO=30°,OP=3,BO=6,
∴⊙O的半径OB为6.
(3)S弓形BQD=S扇形-S△BOD=![]() ×
×![]() ×62 =6π-9
×62 =6π-9![]() .
.


科目:初中数学 来源: 题型:
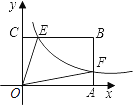
【题目】如图,已知双曲线 ![]() (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= ![]() CB,AF=
CB,AF= ![]() AB,且四边形OEBF的面积为2,则k的值为________.
AB,且四边形OEBF的面积为2,则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.
(1)分别求出当2≤x≤4时,三个函数:y=2x+1,y= ![]() ,y=2(x-1)2+1的最大值和最小值.
,y=2(x-1)2+1的最大值和最小值.
(2)对于二次函数y=2(x-m)2+m-2,当2≤x≤4时有最小值为1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作一个圆,使它经过已知点![]() 和
和![]() ,并且圆心在已知直线
,并且圆心在已知直线![]() 上.
上.
(1)当直线![]() 和
和![]() 相交时,可作几个?
相交时,可作几个?
(2)当直线![]() 和
和![]() 垂直但不经过
垂直但不经过![]() 的中点时,可作出几个?
的中点时,可作出几个?
(3)你还能提出不同于(1),(2)的问题吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
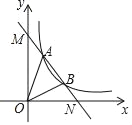
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() >0中x的取值范围;
>0中x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
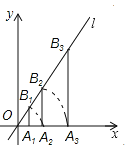
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com