
分析 设A款式服装分配到甲店铺为x件,则分配到乙店铺为(36-x)件;B款式分配到甲店铺为(30-x)件,分配到乙店铺为(x-6)件,总利润为y元,依题意可得到一个等式和一个不等式,可求解.
解答 解:(1)设A款式服装分配到甲店铺为x件,则分配到乙店铺为(36-x)件;
B款式分配到甲店铺为(30-x)件,分配到乙店铺为(x-6)件.
根据题意得:30x+35×(30-x)=26×(36-x)+36(x-6),
解得x=22.
所以36-x=14(件),30-x=8(件),x-6=16(件),
故A款式服装分配到甲店铺为22件,则分配到乙店铺为14件;B款式分配到甲店铺为8件,分配到乙店铺为16件,能使两个店铺在销售完这批服装后所获利润相同;
(2)设总利润为w元,根据题意得:
30x+35×(30-x)≥950,解得x≤20.
解得6≤x≤20.
w=30x+35×(30-x)+26×(36-x)+36(x-6)
=5x+1770,
∵k=5>0,∴w随x的增大而增大,
∴当x=20时,w有最大值1870.
∴A款式服装分配给甲、乙两店铺分别为20件和16件,B款式服装分配给甲、乙两店铺分别为10件和14件,最大的总利润是1870元.
点评 本题涉及了一元一次方程、不等式组和一次函数与实际问题,该题是常考题,分析时较为复杂,要求学生读懂题意,列出提纲,再根据量与量之间的关系列出关系式,由关系式分析最佳方案.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
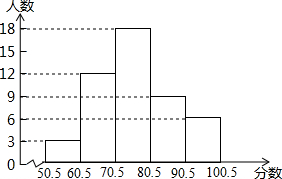 某校一次知识竞赛,竞赛成绩(取整数),进行整理后分五组,并绘制成频数分布直方图,结合图形,解答下列问题:
某校一次知识竞赛,竞赛成绩(取整数),进行整理后分五组,并绘制成频数分布直方图,结合图形,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 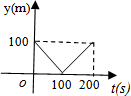 | B. | 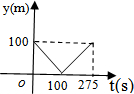 | C. | 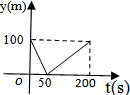 | D. | 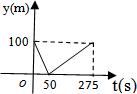 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
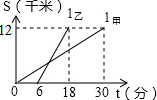 甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走$\frac{3}{5}$千米.
甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走$\frac{3}{5}$千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
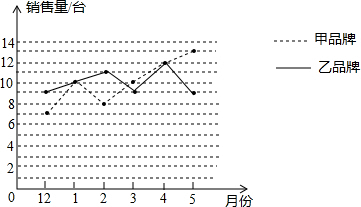
| 平均数 | 方差 | |
| 甲品牌销售量/台 | 10 | $\frac{13}{3}$ |
| 乙品牌销售量/台 | 10 | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
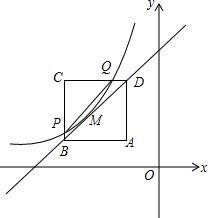 如图,正方形ABCD中A(-1,1),B(-3,1),D(-1,3).反比例函数y=$\frac{k}{x}(x<0)$的图象经过对角线BD的中点M,与BC、CD的边分别交于点P、Q.
如图,正方形ABCD中A(-1,1),B(-3,1),D(-1,3).反比例函数y=$\frac{k}{x}(x<0)$的图象经过对角线BD的中点M,与BC、CD的边分别交于点P、Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
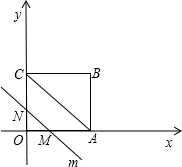 如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com