
【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:

(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
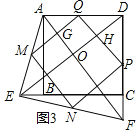
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
【答案】(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.
【解析】
试题(1)因为四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE(SAS),即可得到AF=DE,∠DAF=∠CDE,又因为∠ADG+∠EDC=90°,即有AF⊥DE;
(2)∵四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE(SAS),即可得到AF=DE,∠E=∠F,又因为∠ADG+∠EDC=90°,即有AF⊥DE;
(3)设MQ,DE分别交AF于点G,O,PQ交DE于点H,因为点M,N,P,Q分别为AE,EF,FD,AD的中点,可得MQ=PN=![]() DE,PQ=MN=
DE,PQ=MN=![]() AF,MQ∥DE,PQ∥AF,然后根据AF=DE,可得四边形MNPQ是菱形,又因为AF⊥DE即可证得四边形MNPQ是正方形.
AF,MQ∥DE,PQ∥AF,然后根据AF=DE,可得四边形MNPQ是菱形,又因为AF⊥DE即可证得四边形MNPQ是正方形.
试题解析:(1)上述结论①,②仍然成立,理由是:
∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°,在△ADF和△DCE中,∵DF=CE,∠ADC=∠BCD=90°,AD=CD,∴△ADF≌△DCE(SAS),∴AF=DE,∠DAF=∠CDE,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE;
(2)上述结论①,②仍然成立,理由是:
∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°,在△ADF和△DCE中,∵DF=CE,∠ADC=∠BCD=90°,AD=CD,∴△ADF≌△DCE(SAS),∴AF=DE,∠E=∠F,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE;
(3)四边形MNPQ是正方形.理由是:
如图,设MQ,DE分别交AF于点G,O,PQ交DE于点H,∵点M,N,P,Q分别为AE,EF,FD,AD的中点,
∴MQ=PN=![]() DE,PQ=MN=
DE,PQ=MN=![]() AF,MQ∥DE,PQ∥AF,∴四边形OHQG是平行四边形,∵AF=DE,∴MQ=PQ=PN=MN,∴四边形MNPQ是菱形,∵AF⊥DE,∴∠AOD=90°,∴∠HQG=∠AOD=90°,∴四边形MNPQ是正方形.
AF,MQ∥DE,PQ∥AF,∴四边形OHQG是平行四边形,∵AF=DE,∴MQ=PQ=PN=MN,∴四边形MNPQ是菱形,∵AF⊥DE,∴∠AOD=90°,∴∠HQG=∠AOD=90°,∴四边形MNPQ是正方形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知直线
中,已知直线 ![]() (
( ![]() )分别交反比例函数
)分别交反比例函数 ![]() 和
和 ![]() 在第一象限的图象于点
在第一象限的图象于点 ![]() ,
, ![]() ,过点
,过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() ,交
,交 ![]() 的图象于点
的图象于点 ![]() ,连结
,连结 ![]() .若
.若 ![]() 是等腰三角形,则
是等腰三角形,则 ![]() 的值是 .
的值是 . 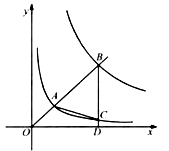
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售某种玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:

(1)小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永州市在进行“六城同创”的过程中,决定购买![]() 两种树对某路段进行绿化改造,若购买
两种树对某路段进行绿化改造,若购买![]() 种树2棵,
种树2棵, ![]() 种树3棵,需要2700元;购买
种树3棵,需要2700元;购买![]() 种树4棵,
种树4棵, ![]() 种树5棵,需要4800元.
种树5棵,需要4800元.
(1)求购买![]() 两种树每棵各需多少元?
两种树每棵各需多少元?
(2)考虑到绿化效果,购进A种树不能少于48棵,且用于购买这两种树的资金不低于52500元.若购进这两种树共100棵.问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”. 
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017
B.2016
C.191
D.190
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为-7、-1、3,乙袋中的三张卡片上所标的数值分别为-2、1、6.先从甲袋中随机取出一张卡片,用 ![]() 表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用
表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用 ![]() 表示取出的卡片上标的数值,把
表示取出的卡片上标的数值,把 ![]() 、
、 ![]() 分别作为点
分别作为点 ![]() 的横坐标、纵坐标.
的横坐标、纵坐标.
(1)用适当的方法写出点 ![]() 的所有情况;
的所有情况;
(2)求点 ![]() 落在第三象限的概率.
落在第三象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com