
【题目】阅读下面材料:

(1)小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
【答案】(1)∠EOF=∠BEO+∠DFO;(2)∠P=65°;(3)∠M=90°﹣![]() α.
α.
【解析】
(1)根据平行线的性质求出∠EOM=∠BEO,∠FOM=∠DFO,即可得出答案;
(2)由DF∥BC,AC∥EF,推出∠EDF=∠B=50°,∠F=∠CGF,推出∠DEF+∠F=180°-50°=130°,再由三角形内角和定理可得∠P+∠FGP=∠F+∠FEP,由此即可解决问题;
(3)由∠M=∠FBM+∠CEM=![]() ∠FBC+
∠FBC+![]() ∠CEM=
∠CEM=![]() (180°-α)=90°-
(180°-α)=90°-![]() α即可解决问题
α即可解决问题
(1)如图1中,
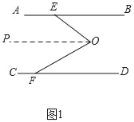
∵OP∥AB,
∴∠EOP=∠BEO,
∵AB∥CD,
∴OP∥CD,
∴∠FOP=∠DFO,
∴∠EOP+∠FOP=∠BEO+∠DFO,
即:∠EOF=∠BEO+∠DFO,
故答案为:∠EOF=∠BEO+∠DFO;
(2)如图2中,
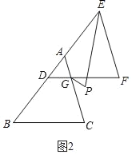
∵DF∥BC,AC∥EF,
∴∠EDF=∠B=50°,∠F=∠CGF,
∴∠DEF+∠F=180°﹣50°=130°,
∵∠P+∠FGP=∠F+∠FEP,
∴∠P=∠F+∠FEP﹣∠FGP=![]() ∠DEF+
∠DEF+![]() ∠F=65°;
∠F=65°;
(3)如图3中,
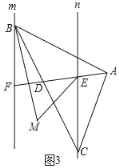
易知∠M=∠FBM+∠CEM,
∵BF∥EC,
∴∠DCE=∠DBF,
∵∠DEC+∠DCE=180°﹣α,
∠M=∠FBM+∠CEM=![]() ∠FBC+
∠FBC+![]() ∠CED=
∠CED=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α.
α.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
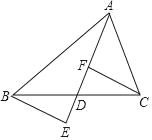
(1)求证:DE=DF;
(2)若在原有条件基础上再添加AB=AC,你还能得出什么结论.(不用证明)(写2个)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为 ![]() 元∕件的玩具以
元∕件的玩具以 ![]() 元∕件的价格出售时,每天可售出
元∕件的价格出售时,每天可售出 ![]() 件,经调查当单价每涨
件,经调查当单价每涨 ![]() 元时,每天少售出
元时,每天少售出 ![]() 件.若商场想每天获得
件.若商场想每天获得 ![]() 元利润,则每件玩具应涨多少元?若设每件玩具涨
元利润,则每件玩具应涨多少元?若设每件玩具涨 ![]() 元,则下列说法错误的是( )
元,则下列说法错误的是( )
A.涨价后每件玩具的售价是 ![]() 元
元
B.涨价后每天少售出玩具的数量是 ![]() 件
件
C.涨价后每天销售玩具的数量是 ![]() 件
件
D.可列方程为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:

(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
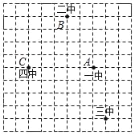
【题目】某同学用10×10的方形网格绘制了遵义市四所初级中学(黑色格点)的位置图.(平方单位)
(1)请在适当的位置建立平面直角坐标系,并根据该平面直角坐标系解答下列问题;
(2)分别写出四所中学所在位置的坐标:一中 ,二中 ,三中 ,四中 ;
(3)分别记一中A、二中B、四中C,移动“三中”的位置于点D(请自行在图中标记),连接A、B、C、D四点组成的四边形ABCD为平行四边形.
①移动后所得D点的坐标是 (写一个点);
②求所得平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2, ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com