
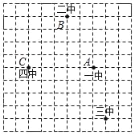
【题目】某同学用10×10的方形网格绘制了遵义市四所初级中学(黑色格点)的位置图.(平方单位)
(1)请在适当的位置建立平面直角坐标系,并根据该平面直角坐标系解答下列问题;
(2)分别写出四所中学所在位置的坐标:一中 ,二中 ,三中 ,四中 ;
(3)分别记一中A、二中B、四中C,移动“三中”的位置于点D(请自行在图中标记),连接A、B、C、D四点组成的四边形ABCD为平行四边形.
①移动后所得D点的坐标是 (写一个点);
②求所得平行四边形ABCD的面积.
科目:初中数学 来源: 题型:
【题目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=﹣1(a<b)的两根,则实数x1 , x2 , a,b的大小关系是( )
A.a<x1<x2<b
B.x1<a<x2<b
C.x1<a<b<x2
D.x1<x2<a<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售某种玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:

(1)小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永州市在进行“六城同创”的过程中,决定购买![]() 两种树对某路段进行绿化改造,若购买
两种树对某路段进行绿化改造,若购买![]() 种树2棵,
种树2棵, ![]() 种树3棵,需要2700元;购买
种树3棵,需要2700元;购买![]() 种树4棵,
种树4棵, ![]() 种树5棵,需要4800元.
种树5棵,需要4800元.
(1)求购买![]() 两种树每棵各需多少元?
两种树每棵各需多少元?
(2)考虑到绿化效果,购进A种树不能少于48棵,且用于购买这两种树的资金不低于52500元.若购进这两种树共100棵.问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
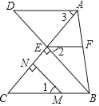
【题目】如图,BE⊥AC与点E,MN⊥AC于点N,∠1=∠2,∠3=∠C,若∠AFE=80°,求∠DAF的度数.请根据解题过程“填空”或“说明理由”.
解:∵BE⊥AC,MN⊥AC
∴BE∥MN
∴∠1= ( )
又∵∠1=∠2
∴∠2= ( )
∴EF∥BC( )
∵∠3=∠C
∴AD∥BC
∴AD∥EF
∴∠DAF+∠AFE=180°( )
∴∠DAF=180°﹣∠AFE=180°﹣80°=100°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”. 
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017
B.2016
C.191
D.190
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() 与
与 ![]() 轴、
轴、 ![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与 ![]() 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com