
【题目】某超市销售某种玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为元.
【答案】40
【解析】解:设销售单价应定为x元,根据题意可得:
利润=(x﹣20)[400﹣10(x﹣30)]
=(x﹣20)(700﹣10x)
=﹣10x2+900x﹣14000
=﹣10(x﹣45)2+6250,
∵超市要完成不少于300件的销售任务,
∴400﹣10(x﹣30)≥300,
解得:x≤40,
即x=40时,销量为300件,此时利润最大为:﹣10(40﹣45)2+6250=6000(元),
故销售单价应定为40元.
故答案为:40.
根据利润=销售量![]() 每件的利润,列出函数解析式,通过配方化成顶点式,再根据要完成不少于300件的销售任务,求出自变量的取值范围,然后根据二次函数的性质即可得出答案。
每件的利润,列出函数解析式,通过配方化成顶点式,再根据要完成不少于300件的销售任务,求出自变量的取值范围,然后根据二次函数的性质即可得出答案。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=﹣x+1(0≤x≤10)与反比例函数y= ![]() (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
A.﹣ ![]() ≤x≤1
≤x≤1
B.﹣ ![]() ≤x≤
≤x≤ ![]()
C.﹣ ![]() ≤x≤
≤x≤ ![]()
D.1≤x≤ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通程电器商城购![]() 台空调、
台空调、![]() 台彩电需花费
台彩电需花费![]() 万元.购
万元.购![]() 台空调、
台空调、![]() 台彩电需花费
台彩电需花费![]() 万元.
万元.
(1)计算每台空调与彩电的进价分别是多少元?
(2)已知一次性购进空调、彩电共![]() 台,购进资金不超过
台,购进资金不超过![]() 万元,购进空调不少于
万元,购进空调不少于![]() 台,写出符合要求的进货方案;
台,写出符合要求的进货方案;
(3)在(2)的情况下,原每台空调的售价为![]() 元.每台彩电的售价为
元.每台彩电的售价为![]() 元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利
元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利![]() 元
元![]() .设商城计划购进空调
.设商城计划购进空调![]() 台,空调和彩电全部销售完商城获得的利润为
台,空调和彩电全部销售完商城获得的利润为![]() 元.试写出
元.试写出![]() 与
与![]() 的函数关系式,选择哪种进货方案,商城获利最大?
的函数关系式,选择哪种进货方案,商城获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为 ![]() 元∕件的玩具以
元∕件的玩具以 ![]() 元∕件的价格出售时,每天可售出
元∕件的价格出售时,每天可售出 ![]() 件,经调查当单价每涨
件,经调查当单价每涨 ![]() 元时,每天少售出
元时,每天少售出 ![]() 件.若商场想每天获得
件.若商场想每天获得 ![]() 元利润,则每件玩具应涨多少元?若设每件玩具涨
元利润,则每件玩具应涨多少元?若设每件玩具涨 ![]() 元,则下列说法错误的是( )
元,则下列说法错误的是( )
A.涨价后每件玩具的售价是 ![]() 元
元
B.涨价后每天少售出玩具的数量是 ![]() 件
件
C.涨价后每天销售玩具的数量是 ![]() 件
件
D.可列方程为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:

(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
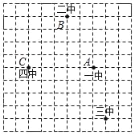
【题目】某同学用10×10的方形网格绘制了遵义市四所初级中学(黑色格点)的位置图.(平方单位)
(1)请在适当的位置建立平面直角坐标系,并根据该平面直角坐标系解答下列问题;
(2)分别写出四所中学所在位置的坐标:一中 ,二中 ,三中 ,四中 ;
(3)分别记一中A、二中B、四中C,移动“三中”的位置于点D(请自行在图中标记),连接A、B、C、D四点组成的四边形ABCD为平行四边形.
①移动后所得D点的坐标是 (写一个点);
②求所得平行四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com