
分析 变形x+2y+3z=0为x+2y=-3z,利用等式两边立方也相等,化简后约分求值.
解答 解:∵x+2y+3z=0,所以x+2y=-3z,
所以(x+2y)3=(-3z)3,即x3+6x2y+12xy2+8y3=-27z3,
∴x3+8y3=-27z3-(6x2y+12xy2)
∴原式=$\frac{-27{z}^{3}-(6{x}^{2}y+12x{y}^{2})+27{z}^{3}}{xyz}$=$\frac{-6xy(x+2y)}{xyz}$=$\frac{-6(x+2y)}{z}=\frac{-6(-3z)}{z}=18$.
故答案为:18.
点评 本题考查了立方根公式及分式约分的相关知识.解决本题的关键是变形已知,代入它们的立方.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
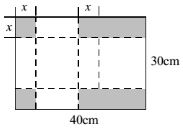 把长为40cm,宽为30cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),把剩余部分折成一个有盖的长方体盒子,记剪掉的小的正方形边长为x cm,(纸板的厚度忽略不计)若折成的长方体盒子表面积为950cm2,求此时长方体盒子的体积为1500cm3.
把长为40cm,宽为30cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),把剩余部分折成一个有盖的长方体盒子,记剪掉的小的正方形边长为x cm,(纸板的厚度忽略不计)若折成的长方体盒子表面积为950cm2,求此时长方体盒子的体积为1500cm3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com