
分析 (1)根据横坐标,右移加,左移减;纵坐标,上移加,下移减进行计算;
(2)设直线l的解析式为y=kx+b,再把(2,1),(4,-2)代入可得关于k、b的方程组,解方程得到k、b的值,进而可得直线l的解析式.
解答 解:(1)点P1(2,1)先向右平移2个单位,再向下平移3个单位得到点P2(4,-2);
(2)设直线l的解析式为y=kx+b,
∵直线经过(2,1),(4,-2),
∴$\left\{\begin{array}{l}{2k+b=1}\\{4k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=4}\end{array}\right.$,
∴直线l的解析式为y=-$\frac{3}{2}$x+4.
点评 此题主要考查了一次函数图象与几何变换,关键是掌握待定系数法求一次函数解析式一般步骤是:
(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;
(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;
(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
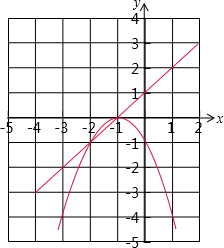 设函数y=(x+1)[(k-2)x+(2k-3)](k是常数).
设函数y=(x+1)[(k-2)x+(2k-3)](k是常数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
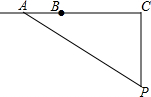 如图,l为一条东西方向的笔直公路,一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A、B、C,P是一个观测点,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,测得该车从点A行驶到点B所用时间为1秒.
如图,l为一条东西方向的笔直公路,一辆小汽车XRS在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A、B、C,P是一个观测点,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,测得该车从点A行驶到点B所用时间为1秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知O是坐标原点,A、B的坐标分别为(3,1),(2,-1).
如图,已知O是坐标原点,A、B的坐标分别为(3,1),(2,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com