
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїDEFЪЧСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=ЁЯEDF=90ЁуЃЌЁїDEFЕФЖЅЕуEгыЁїABCЕФаББпBCЕФжаЕужиКЯЃЎНЋЁїDEFШЦЕуEа§зЊЃЌа§зЊЙ§ГЬжаЃЌЯпЖЮDEгыЯпЖЮABЯрНЛгкЕуPЃЌЯпЖЮEFгыЩфЯпCAЯрНЛгкЕуQЃЎ
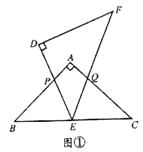
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕуQдкЯпЖЮACЩЯЃЌЧвAP=AQЪБЃЌЧѓжЄЃКЁїBPEЁеЁїCQEЃЛ
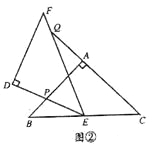
ЃЈ2ЃЉШчЭМЂкЃЌЕБЕуQдкЯпЖЮCAЕФбгГЄЯпЩЯЪБЃЌЧѓжЄЃКЁїBPEЁзЁїCEQЃЛВЂЧѓЕБBP= ![]() ЃЌCQ=
ЃЌCQ= ![]() ЪБЃЌPЁЂQСНЕуМфЕФОрРы (гУКЌ
ЪБЃЌPЁЂQСНЕуМфЕФОрРы (гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЎ
ЕФДњЪ§ЪНБэЪО)ЃЎ
ЁОД№АИЁПЃЈ1ЃЉгЩЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌвзЕУЁЯB=ЁЯC=45ЁуЃЌAB=ACЃЌгжгЩAP=AQЃЌEЪЧBCЕФжаЕуЃЌРћгУSASЃЌПЩжЄЕУЁїBPEЁеЁїCQEЃЛ
ЃЈ2ЃЉгЩЁїABCКЭЁїDEFЪЧСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌвзЕУЁЯB=ЁЯC=ЁЯDEF=45ЁуЃЌШЛКѓРћгУШ§НЧаЮЕФЭтНЧЕФаджЪЃЌМДПЩЕУЁЯBEP=ЁЯEQCЃЌдђПЩжЄЕУЁїBPEЁзЁїCEQЃЛPQ=![]() a
a
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌвзЕУЁЯB=ЁЯC=45ЁуЃЌAB=ACЃЌгжгЩAP=AQЃЌEЪЧBCЕФжаЕуЃЌРћгУSASЃЌПЩжЄЕУЃКЁїBPEЁеЁїCQEЃЛ
ЃЈ2ЃЉгЩЁїABCКЭЁїDEFЪЧСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌвзЕУЁЯB=ЁЯC=ЁЯDEF=45ЁуЃЌШЛКѓРћгУШ§НЧаЮЕФЭтНЧЕФаджЪЃЌМДПЩЕУЁЯBEP=ЁЯEQCЃЌдђПЩжЄЕУЃКЁїBPEЁзЁїCEQЃЛИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУBEЕФГЄЃЌМДПЩЕУBCЕФГЄЃЌМЬЖјЧѓЕУAQгыAPЕФГЄЃЌРћгУЙДЙЩЖЈРэМДПЩЧѓЕУPЁЂQСНЕуМфЕФОрРыЃЎ
ЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯB=ЁЯC=45ЁуЃЌAB=ACЃЌ
ЁпAP=AQЃЌ
ЁрBP=CQЃЌ
ЁпEЪЧBCЕФжаЕуЃЌ
ЁрBE=CEЃЌ
ЁрЁїBPEЁеЁїCQEЃЈSASЃЉЃЛ
ЃЈ2ЃЉСЌНгPQ
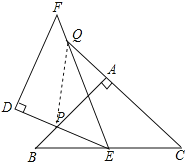
ЁпЁїABCКЭЁїDEFЪЧСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯB=ЁЯC=ЁЯDEF=45ЁуЃЌ
ЁпЁЯBEQ=ЁЯEQC+ЁЯCЃЌМДЁЯBEP+ЁЯDEF=ЁЯEQC+ЁЯCЃЌ
ЁрЁЯBEP+45Ёу=ЁЯEQC+45ЁуЃЌ
ЁрЁЯBEP=ЁЯEQCЃЌ
ЁрЁїBPEЁзЁїCEQЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпBP=aЃЌCQ=![]() aЃЌBE=CEЃЌ
aЃЌBE=CEЃЌ
Ёр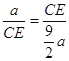 ЃЌ
ЃЌ
ЁрBE=CE=![]() ЃЌ
ЃЌ
ЁрBC=3![]() ЃЌ
ЃЌ
ЁрAB=AC=BCsin45Ёу=3aЃЌ
ЁрAQ=CQ-AC=![]() ЃЌPA=AB-BP=2aЃЌ
ЃЌPA=AB-BP=2aЃЌ
![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌШєЕуPЃЈmЃЋ3ЃЌЃ2mЃЉЕНСНзјБъжсЕФОрРыЯрЕШЃЌдђmЕФжЕЮЊЃЈ ЃЉ
A.Ѓ1B.3C.Ѓ1Лђ3D.Ѓ1Лђ5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєxa+2y4гыЉ3x3y2bЪЧЭЌРрЯюЃЌдђ2018ЃЈaЉbЃЉ2018ЕФжЕЪЧЃЈЁЁЁЁЃЉ
A. 2018 B. 1 C. Љ1 D. Љ2018
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуMЃЈЉ3ЃЌ2ЃЉЙигкyжсЖдГЦЕФЕуЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A.ЃЈЉ3ЃЌЉ2ЃЉB.ЃЈЉ2ЃЌЉ3ЃЉC.ЃЈ3ЃЌ2ЃЉD.ЃЈ3ЃЌЉ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛжЛаЁГцДгЕуAЃЈЉ2ЃЌ1ЃЉГіЗЂЃЌЯШЯђгвЬј4ИіЕЅЮЛЃЌдйЯђЯТЬј3ИіЕЅЮЛЃЌЕНДяЕуBДІЃЌдђЕуBЕФзјБъЪЧЃЈ ЃЉ
A.ЃЈЉ5ЃЌ5ЃЉ
B.ЃЈ2ЃЌЉ2ЃЉ
C.ЃЈ1ЃЌ5ЃЉ
D.ЃЈ2ЃЌ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋ4ИіЪ§aЃЌbЃЌcЃЌdХХГЩ2ааЁЂ2СаЃЌСНБпИїМгвЛЬѕЪњжБЯпМЧГЩ![]() ЃЌЖЈвх
ЃЌЖЈвх![]() ЃНadЃbcЃЌЩЯЪіМЧКХОЭНазі2НзааСаЪНЃЎШє
ЃНadЃbcЃЌЩЯЪіМЧКХОЭНазі2НзааСаЪНЃЎШє![]() ЃНЃ20ЃЌЧѓxЕФжЕЃЎ
ЃНЃ20ЃЌЧѓxЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТУцЕФЕуеѓЭМКЭЯргІЕФЕШЪНЃЌЬНОПЦфжаЕФЙцТЩЃК
ЃЈ1ЃЉдкЂмКЭЂнКѓУцЕФКсЯпЩЯЗжБ№аДГіЯргІЕФЕШЪНЃЛ

Ђм__________________________________________________________ЃЛЂн_____________________________________________________ЃЛ
ЃЈ2ЃЉИљОнЩЯУцЫуЪНЕФЙцТЩЃЌЧыМЦЫуЃК ![]() ________________________ЃЛ
________________________ЃЛ
ЃЈ3ЃЉЭЈЙ§ВТЯыаДГігыЕкnИіЕуеѓЯрЖдгІЕФЕШЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧаЁУїЩшМЦЕФжЧСІЦДЭМЭцОпЃЌЯждкаЁУїгіЕНСЫЯТУцСНИіЮЪЬтЃЌЧыФуАяжњНтОі.
(1)ШчЭМЂХЃЌЁЯD=![]() ,ЁЯACD=
,ЁЯACD=![]() .ЮЊБЃжЄABЁЮDE,ЁЯAгІЕШгкЖрЩйЖШЃП
.ЮЊБЃжЄABЁЮDE,ЁЯAгІЕШгкЖрЩйЖШЃП
(2)ШчЭМЂЦЃЌШєGPЁЮHQ,дђЁЯG,ЁЯF, ЁЯHжЎМфгаЪВУДбљЕФЙиЯЕЃП
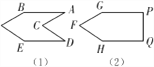
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіШ§НЧаЮШЮвтвЛБпЩЯЕФИпЖМЪЧетБпЩЯЕФжаЯпЃЌдђЖдетИіШ§НЧаЮзюзМШЗЕФХаЖЯЪЧЃЈ ЃЉ
A.ЕШбќШ§НЧаЮB.жБНЧШ§НЧаЮC.е§Ш§НЧаЮD.ЕШбќжБНЧШ§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com