
| A. | $\sqrt{12}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\sqrt{{a}^{2}{b}^{3}}$ | D. | $\sqrt{\frac{a}{2}}$ |
分析 直接利用最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.我们把满足上述两个条件的二次根式,叫做最简二次根式,进而得出答案.
解答 解:A、$\sqrt{12}$=2$\sqrt{3}$,不是最简二次根式,故此选项错误;
B、$\sqrt{{a}^{2}+{b}^{2}}$,是最简二次根式,故此选项正确;
C、$\sqrt{{a}^{2}{b}^{3}}$=|ab|$\sqrt{b}$,不是最简二次根式,故此选项错误;
D、$\sqrt{\frac{a}{2}}$=$\frac{\sqrt{2a}}{2}$,不是最简二次根式,故此选项错误.
故选:B.
点评 此题主要考查了最简二次根式的定义,正确把握定义是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
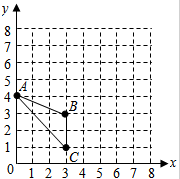 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有两个可以自由转动的均匀转盘,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:分别转动转盘,两个转盘停止后,将两个指针所指份内的数字相乘,(若指针停止在等分线上,那么重转一次,直到指针指向某份为止).
有两个可以自由转动的均匀转盘,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:分别转动转盘,两个转盘停止后,将两个指针所指份内的数字相乘,(若指针停止在等分线上,那么重转一次,直到指针指向某份为止).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:判断题
已知:二次函数 的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com