
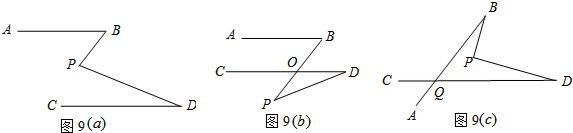
分析 (1)过点P作PE∥AB,由平行线的性质“两直线平行,内错角相等”得出∠B=∠BPE、∠D=∠DPE,结合角之间的关系即可得出结论;
(2)过点P作PE∥CD,根据平行线的性质即可得出∠BOD=∠BPE、∠D=∠DPE,结合角之间的关系即可得出结论;
(3)数量关系:∠BPD=∠B+∠BQD+∠D.过点P作PE∥CD,过点B作BF∥PE,由平行线的性质得出“∠FBA+∠BQD=180°,∠FBP+∠BPE=180°,∠D=∠DPE”,再根据角之间的关系即可得出结论.
解答 (1)证明:过点P作PE∥AB,如图1所示.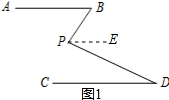
∵AB∥PE,AB∥CD,(已知)
∴AB∥PE∥CD.(在同一平面内,平行于同一直线的两条直线互相平行)
∴∠B=∠BPE,∠D=∠DPE,(两直线平行,内错角相等)
∴∠BPD=∠BPE+∠DPE=∠B+∠D.(等量代换)
(2)证明:过点P作PE∥CD,如图2所示.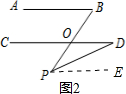
∵PE∥CD,(辅助线)
∴∠BOD=∠BPE,(两直线平行,同位角相等);∠D=∠DPE,(两直线平行,内错角相等)
∴∠BPE=∠BPD+∠DPE=∠BPD+∠D,(等量代换)
即∠BOD=∠P+∠D.(等量代换)
(3)解:数量关系:∠BPD=∠B+∠BQD+∠D.
理由如下:
过点P作PE∥CD,过点B作BF∥PE,如图3所示.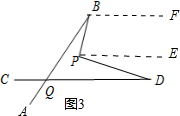
则BF∥PE∥CD,
∴∠FBA+∠BQD=180°,∠FBP+∠BPE=180°,(两直线平行,同旁内角互补)
∠D=∠DPE,(两直线平行,内错角相等)
∵∠FBA=∠FBP+∠B,
∴∠BPE=∠BQD+∠B,
∴∠BPD=∠BPE+∠DPE=∠BQD+∠B+∠D.(等量代换)
点评 本题考查了平行线的性质以及角的计算,解题的关键是根据平行线的性质找出相等或互补的角.本题属于中档题,(1)难度不大;(2)(3)在实际做题中完全可以利用三角形外角的性质来解决问题,平行线的性质是很简单,但是很多时候用反而不如不用好.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5{x}^{3}}$ | B. | $\sqrt{4m}$ | C. | $\sqrt{{a}^{2}+3}$ | D. | $\sqrt{\frac{1}{x}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
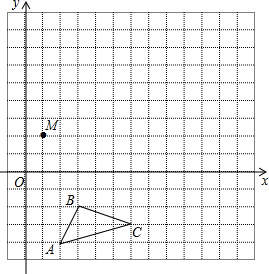 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
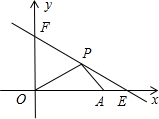 已知:如图,直线y=kx+b与x轴y轴分别交于点E,F,点E,F的坐标为(8,0),(0,6),点A的坐标为(6,0).
已知:如图,直线y=kx+b与x轴y轴分别交于点E,F,点E,F的坐标为(8,0),(0,6),点A的坐标为(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\sqrt{{a}^{2}{b}^{3}}$ | D. | $\sqrt{\frac{a}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com