
����Ŀ����ͼ��A��B���������ֱ��ǣ�8��0������0��6������P�ɵ�B������BA�������A������ֱ���˶����ٶ�Ϊÿ��3����λ���ȣ���Q��A������AO��OΪ����ԭ�㣩�������O������ֱ���˶����ٶ�Ϊÿ��2����λ���ȣ�����PQ�������˶�ʱ��Ϊt��0��t��![]() ���룮����������⣺
���룮����������⣺
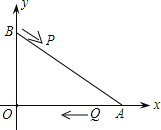
��1����tΪ��ֵʱ��PQ��BO��
��2������AQP�����ΪS��
����S��t֮��ĺ�����ϵʽ�������S�����ֵ��
�������ǹ涨����P��Q������ֱ�Ϊ��x1��y1������x2��y2�����������꣨x2��x1��y2��y1����Ϊ������PQ�������꣮��Sȡ���ֵʱ��������PQ�������꣮
���𰸡���1����t=![]() ��ʱ��PQ��BO��2����S=
��ʱ��PQ��BO��2����S=![]() ��0��t��
��0��t��![]() ����5����
����5����![]() ����3��
����3��
���������⣺��1����A��B���������ֱ��ǣ�8��0������0��6������OB=6��OA=8��
��![]() ��
��
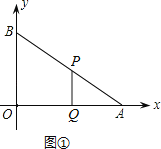
��ͼ������PQ��BOʱ��AQ=2t��BP=3t����AP=10��3t��
��PQ��BO����![]() ����
����![]() �����t=
�����t=![]() ��
��
����t=![]() ��ʱ��PQ��BO��
��ʱ��PQ��BO��
��2���ɣ�1��֪��OA=8��OB=6��AB=10��
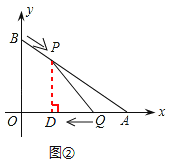
����ͼ����ʾ������P��PD��x���ڵ�D��
��PD��BO��
����APD�ס�ABO��
��![]() ����
����![]() �����PD=6��
�����PD=6��![]() t��
t��
��![]() ��
��
��S��t֮��ĺ�����ϵʽΪ��S=![]() ��0��t��
��0��t��![]() ����
����
����t=![]() ��ʱ��Sȡ�����ֵ�����ֵΪ5��ƽ����λ����
��ʱ��Sȡ�����ֵ�����ֵΪ5��ƽ����λ����
����ͼ����ʾ����Sȡ���ֵʱ��t=![]() ��
��
��PD=6��![]() t=3����PD=
t=3����PD=![]() BO��
BO��
��PD��BO������ʱPDΪ��OAB����λ�ߣ���OD=![]() OA=4����P��4��3����
OA=4����P��4��3����
��AQ=2t=![]() ����OQ=OA��AQ=
����OQ=OA��AQ=![]() ����Q��
����Q��![]() ��0����
��0����
�����⣬������PQ��������Ϊ��![]() ��4��0��3��������
��4��0��3��������![]() ����3����
����3����
����Sȡ���ֵʱ��������PQ��������Ϊ��![]() ����3����
����3����
��1����ͼ����ʾ����PQ��BOʱ������ƽ���߷��߶γɱ������������߶α���ʽ![]() �����t��ֵ��
�����t��ֵ��
��2������S��ϵʽ��Ҫ���������AQP�ĸߣ���ͼ����ʾ������P������P��PD��x���ڵ�D������ƽ����PD��BO������APD�ס�ABO�� ![]() ���PD���Ӷ�S�������S��t֮��ĺ�����ϵʽ��һ������t�Ķ��κ��������ö��κ�����ֵ�ķ������S�����ֵ��
���PD���Ӷ�S�������S��t֮��ĺ�����ϵʽ��һ������t�Ķ��κ��������ö��κ�����ֵ�ķ������S�����ֵ��
�������P��Q����������Sȡ���ֵʱ�����Ƴ���ʱPDΪ��OAB����λ�ߣ��Ӷ��������P���ݺ����꣬������Q�����꣬�Ӷ���õ�P��Q�����ꣻ���P��Q������֮���롰����PQ������Ķ��壨x2��x1��y2��y1�������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��E����AΪԲ�ģ���2Ϊ�뾶��Բ��һ ���㣬����CE����PΪCE���е㣬����BP����AC=![]() ��BD=
��BD=![]() ����BP�����ֵΪ�� ��
����BP�����ֵΪ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������λ����ƽ��ʱ����������ȫƽ��ʽ��������ʽ���ķ����������㣬���������£�
���磺��322��
�⣺��Ϊ(3x��2y)2��9x2��4y2��12xy������ʽ�еȺ��ұߵ�ϵ����������ı����пɵã�
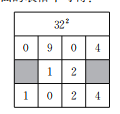
����322��1024��
(1)�����Ǽμη���������892��һ���ֹ��̣����������ȫ�����������
�⣺��Ϊ(8x��9y)2��64x2��81y2��144xy������ʽ�еȺ��ұߵ�ϵ����������ı����пɵã�
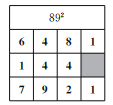
����892�� ��
(2)�������⣬����672��
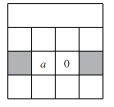
(3)������������ʽ���ķ�������һ����λ����ƽ�������ֹ�����ͼ��ʾ���������λ���ĸ�λ����Ϊa���������λ��Ϊ (�ú�a�Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx��3a������A����1��0����C��0��3������x�ύ����һ��B�������ߵĶ���ΪD��

��1����˶��κ�������ʽ��
��2������DC��BC��DB����֤����BCD��ֱ�������Σ�
��3���ڶԳ����Ҳ�����������Ƿ���ڵ�P��ʹ����PDCΪ���������Σ������ڣ�������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
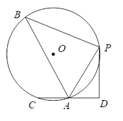
����Ŀ����ͼ���ڡ�O�У�B��P��A��C��Բ�ϵĵ㣬![]() �� PD��CD��CD����O��A����AC=AD��PD =
�� PD��CD��CD����O��A����AC=AD��PD = ![]() ��sin��PAD =
��sin��PAD = ![]() ������PAB�����Ϊ_______��
������PAB�����Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
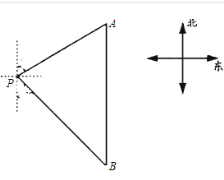
����Ŀ����ͼ,һ���ִ�λ�ڵ���P�ı�ƫ��60�㷽��,�����P�ľ���Ϊ100�����A��,�������Ϸ�����һ��ʱ���,����λ�ڵ���P����ƫ��37�㷽���ϵ�B��,���ʱ�ִ����ڵ�B�������P�ľ���(sin53��=0.8��sin37��=0.6��tan53��=1.3��![]() �����ȷ��0.1).
�����ȷ��0.1).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��AOB�У�AB��OB����AB=OB=3����ֱ��![]() �ش�������������Ӱ���ֵ����ΪS����S��t֮��ĺ�����ϵ��ͼ��Ϊ����ѡ���еģ�������
�ش�������������Ӱ���ֵ����ΪS����S��t֮��ĺ�����ϵ��ͼ��Ϊ����ѡ���еģ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ѧУ�������Ա�����б��CD��һ����AB�ĸ߶ȣ��������ڵ�C���������B������Ϊ 60����Ȼ�����¶�D�������B������Ϊ300����֪б��CD�ij���Ϊ20m��DE�ij�Ϊ10m������AB�ĸ߶��ǣ� �� m

A. ![]() B. 30 C.
B. 30 C. ![]() D. 40
D. 40
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC �У�AB=AC�� ��BAC ��60�㣬���߶� AB �Ƶ� A��ʱ����ת 60��õ��� D�� �� E ��� D ����ֱ�� BC �Գƣ����� CD��CE��DE��
��1�������ⲹȫͼ�Σ�
��2���жϡ�CDE ����״����֤����
��3��������ֱ��CE���Ƿ���ڵ� P��ʹ�� PA - PB =CD �����������ڣ����������������� P ��ȷλ�ã�����ͼ֤�����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com