
【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;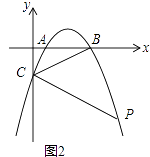
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 ![]() a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.
【答案】
(1)
解:当y=0时,ax2﹣5ax+4a=0,解得x1=1,x2=4,则A(1,0),B(4,0),
∴AB=3,
∵△ABC的面积为3,
∴ ![]() 4OC=3,解得OC=2,则C(0,﹣2),
4OC=3,解得OC=2,则C(0,﹣2),
把C(0,﹣2)代入y=ax2﹣5ax+4a得4a=﹣2,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)
解:过点P作PH⊥x轴于H,作CD⊥PH于点H,如图2,
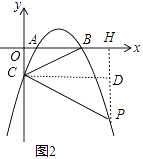
设P(x,ax2﹣5ax+4a),则PD=4a﹣(ax2﹣5ax+4a)=﹣ax2+5ax,
∵AB∥CD,
∴∠ABC=∠BCD,
∵∠BCP=2∠ABC,
∴∠PCD=∠ABC,
∴Rt△PCD∽Rt△CBO,
∴PD:OC=CD:OB,
即(﹣ax2+5ax):(﹣4a)=x:4,解得x1=0,x2=6,
∴点P的横坐标为6
(3)
解:过点F作FG⊥PK于点G,如图3,
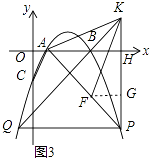
∵AK=FK,
∴∠KAF=∠KFA,
而∠KAF=∠KAH+∠PAH,∠KFA=∠PKF+∠KPF,
∵∠KAH=∠FKP,
∴∠HAP=∠KPA,
∴HA=HP,
∴△AHP为等腰直角三角形,
∵P(6,10a),
∴﹣10a=6﹣1,解得a=﹣ ![]() ,
,
在Rt△PFG中,∵PF=﹣4 ![]() a=2
a=2 ![]() ,∠FPG=45°,
,∠FPG=45°,
∴FG=PG= ![]() PF=2,
PF=2,
在△AKH和△KFG中
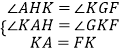 ,
,
∴△AKH≌△KFG,
∴KH=FG=2,
∴K(6,2),
设直线KB的解析式为y=mx+n,
把K(6,2),B(4,0)代入得 ![]() ,
,
解得 ![]() ,
,
∴直线KB的解析式为y=x﹣4,
当a=﹣ ![]() 时,抛物线的解析式为y=﹣
时,抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2,
x﹣2,
解方程组 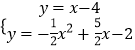 ,
,
解得 ![]() 或
或 ![]() ,
,
∴Q(﹣1,﹣5),
而P(6,﹣5),
∴PQ∥x 轴,
∴QP=7.
【解析】(1)通过解方程ax2﹣5ax+4a=0可得到A(1,0),B(4,0),然后利用三角形面积公式求出OC得到C点坐标,再把C点坐标代入y=ax2﹣5ax+4a中求出a即可得到抛物线的解析式;(2)过点P作PH⊥x轴于H,作CD⊥PH于点H,如图2,设P(x,ax2﹣5ax+4a),则PD=﹣ax2+5ax,通过证明Rt△PCD∽Rt△CBO,利用相似比可得到(﹣ax2+5ax):(﹣4a)=x:4,然后解方程求出x即可得到点P的横坐标;(3)过点F作FG⊥PK于点G,如图3,先证明∠HAP=∠KPA得到HA=HP,由于P(6,10a),则可得到﹣10a=6﹣1,解得a=﹣ ![]() ,再判断Rt△PFG单位等腰直角三角形得到FG=PG=
,再判断Rt△PFG单位等腰直角三角形得到FG=PG= ![]() PF=2,接着证明△AKH≌△KFG,得到KH=FG=2,则K(6,2),然后利用待定系数法求出直线KB的解析式为y=x﹣4,再通过解方程组
PF=2,接着证明△AKH≌△KFG,得到KH=FG=2,则K(6,2),然后利用待定系数法求出直线KB的解析式为y=x﹣4,再通过解方程组 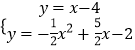 得到Q(﹣1,﹣5),利用P、Q点的坐标可判断PQ∥x 轴,于是可得到QP=7.
得到Q(﹣1,﹣5),利用P、Q点的坐标可判断PQ∥x 轴,于是可得到QP=7.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( ) 
A.汽车在高速公路上的行驶速度为100km/h
B.普通公路总长为90km
C.汽车在普通公路上的行驶速度为60km/h
D.汽车出发后4h到B地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形对角线,请在大长方形中完成下列画图,要求:(1)仅用无刻度直尺;(2)保留必要的画图痕迹.
(1)在图(1)中画一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图(2)中画出线段AB的垂直平分线,并简要说明画图的方法(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE. 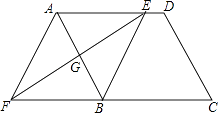
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2 ![]() h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是(填写所有正确结论的序号).
h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是(填写所有正确结论的序号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点,若AE= ![]() ,∠EAF=135°,则下列结论正确的是( )
,∠EAF=135°,则下列结论正确的是( ) 
A.DE=1
B.tan∠AFO= ![]()
C.AF= ![]()
D.四边形AFCE的面积为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com