
【题目】在学习了数轴后,小亮决定对数轴进行变化应用:
(1)应用一:已知点![]() 在数轴上表示为-2,数轴上任意一点
在数轴上表示为-2,数轴上任意一点![]() 表示的数为
表示的数为![]() ,则
,则![]() 两点的距离可以表示为 ;应用这个知识,请写出当
两点的距离可以表示为 ;应用这个知识,请写出当![]() 时,
时,![]() 有最小值为 .
有最小值为 .
(2)应用二:从数轴上取下一个单位长度的线段,第一次剪掉原长的![]() ,第二次剪掉剩下的
,第二次剪掉剩下的![]() ,依此类推,每次都剪掉剩下的
,依此类推,每次都剪掉剩下的![]() ,则剪掉4次后剩下线段长度为 ;应用这个原理,请计算:
,则剪掉4次后剩下线段长度为 ;应用这个原理,请计算:![]() ;
;
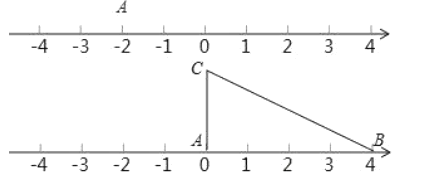
(3)应用三:如图,将一根拉直的细线看作数轴,一个三边长分别为![]() ,
,![]() ,
,![]() 的三角形
的三角形![]() 的顶点
的顶点![]() 与原点重合,
与原点重合,![]() 边在数轴正半轴上,将数轴正半轴的线沿
边在数轴正半轴上,将数轴正半轴的线沿![]() 的顺序依次缠绕在三角形
的顺序依次缠绕在三角形![]() 的边上,负半轴的线沿
的边上,负半轴的线沿![]() 的顺序依次缠绕在三角形
的顺序依次缠绕在三角形![]() 的边上.
的边上.
①如果正半轴的线缠绕了3圈,负半轴的线缠绕了5圈,求绕在点![]() 上的所有数之和;
上的所有数之和;
②如果正半轴的线不变,将负半轴的线拉长一倍,即原线上的点-2的位置对应着拉长后的数-1,并将三角形![]() 向正半轴平移一个单位后再开始绕,求绕在点
向正半轴平移一个单位后再开始绕,求绕在点![]() 且绝对值不超过60的所有数之和.
且绝对值不超过60的所有数之和.
【答案】(1)![]() ,
,![]() ,14;(2)
,14;(2)![]() ,
,![]() ;(3)①
;(3)①![]() ;②-160
;②-160
【解析】
(1)根据数轴上两点间的距离的表示来列式即可;
(2)第一次剪掉的长度是![]() ,剩下的长度是
,剩下的长度是![]() ;第二次剪掉的长度是
;第二次剪掉的长度是![]() ,剩下的长度是
,剩下的长度是![]() ;以此类推,即可求得答案;
;以此类推,即可求得答案;
(3)①分别找出正半轴和负半轴在点C上的数字之间的规律,即可求出所有数字之和;
②分别找出绕在点B且绝对值不超过60的所有数字,求和即可.
(1)已知点A在数轴上表示为![]() ,数轴上任意一点B表示的数为
,数轴上任意一点B表示的数为![]() ,则AB两点的距离可以表示为
,则AB两点的距离可以表示为![]() ;
;
根据![]() 的几何意义,可得:
的几何意义,可得:
![]() 表示
表示![]() 到数轴上
到数轴上![]() ,3,0,5,6五个数的距离之和,
,3,0,5,6五个数的距离之和,
∴当![]() 与
与![]() 重合时,
重合时,![]() 有最小值,最小值为14,此时
有最小值,最小值为14,此时![]() .
.
故答案为:![]() ,
,![]() ,14;
,14;
(2)第一次剪掉的长度是![]() ,剩下的长度是
,剩下的长度是![]() ;
;
第二次剪掉的长度是![]() ,剩下的长度是
,剩下的长度是![]() ;
;
第三次剪掉的长度是![]() ,剩下的长度是
,剩下的长度是![]() ;
;
第四次剪掉的长度是![]() ,剩下的长度是
,剩下的长度是![]() ;
;
![]() ,
,
第八次剪掉的长度是![]() ,剩下的长度是
,剩下的长度是![]() ;
;
∴![]()
![]() ,
,
故答案为:![]() ,
,![]() ;
;
(3)①如果正半轴的线缠绕了5圈,绕在点C的数字分别为:9,21,33,45,57;
负半轴的线缠绕了3圈,绕在点C的数字分别为:-3,-15,-27.
则绕在点C上的所有数字之和为:![]() ;
;
②如果正半轴的线不变,并将三角形ABC向正半轴平移一个单位后再开始绕,
则正半轴上绕在点B且绝对值不超过60的数字有:5,17,29,41,53;
将负半轴的线拉长一倍,并将三角形ABC向正半轴平移一个单位后再开始绕,
则负半轴上绕在点B且绝对值不超过60的数字有:-3.5,-9.5,-15.5,-21.5,-27.5,-33.5,-39.5,-45.5,-51.5,-57.5.
则绕在点B且绝对值不超过60的数字之和为:![]() .
.
故答案为:①![]() ;②
;②![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】为更好地宜传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如下的调查问卷(单选).在随机调查了全市5000名司机中的部分司机后,统计整理并制作了如下的统计图:
克服酒驾——你认为哪一种方式更好?
A.司机酒驾,乘客有责,让乘客帮助监督
B.在汽车上张贴“请勿清驾”的提醒标志
C.希望交警加大检查力度
D.查出酒驾,追究就餐饭店的连带责任
E.查出酒驾,追究同桌吃饭的人的连带责任

根据以上信息解答下列问题:
(1)要补全条形统计图,选项![]() 的人数是____________计算扇形统计图中
的人数是____________计算扇形统计图中![]() =__________.
=__________.
(2)该市司机支持选项![]() 的司机大约有多少人?
的司机大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开住乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间式(小时)之间的函数图象如图所示,则下列说法中错误的是( )
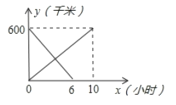
A. 客车比出租车晚4小时到达目的地B. 客车速度为60千米时,出租车速度为100千米/时
C. 两车出发后3.75小时相遇D. 两车相遇时客车距乙地还有225千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,且满足
,且满足![]() ,多项式
,多项式![]() 是五次四项式.
是五次四项式.
(1)则![]() 的值为 ,
的值为 ,![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)已知点![]() 是数轴上的两个动点,点
是数轴上的两个动点,点![]() 从点
从点![]() 出发,以每秒3个单位的速度向右运动,同时点
出发,以每秒3个单位的速度向右运动,同时点![]() 从点
从点![]() 出发,以每秒4个单位的速度向左运动:
出发,以每秒4个单位的速度向左运动:
①若点![]() 和点
和点![]() 经过
经过![]() 秒后,在数轴上的点
秒后,在数轴上的点![]() 处相遇,求
处相遇,求![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
②若点![]() 运动到点
运动到点![]() 处,点
处,点![]() 再出发,则点
再出发,则点![]() 运动几秒后两点之间的距离为8个单位长度.
运动几秒后两点之间的距离为8个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
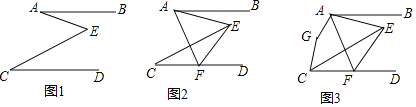
【题目】已知:AB∥CD,平面内有一点E,连接AE、CE
(1)如图1,求证:∠E=∠A+∠C;
(2)如图2,CD上有一点F,连接AF、EF,若∠FAE=∠FEA,∠EFD=2∠C,求证:∠AFC=2∠AEC;
(3)如图3,在(2)的条件下,平面内有一点G,连接AG、CG,若∠GCE与∠GAE互为补角,5∠AFC=2∠G,求∠G的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完善下列解题步辈.井说明解题依据.
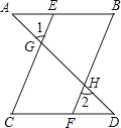
如图,已知∠1=∠2,∠B=∠C,求证:AB∥CD.
证明:∵∠1=∠2(已知)
且∠1=∠CGD(______)
∴∠2=∠CGD(______)
∴______∥______(______),
∴∠C=______(______)
又∵∠B=∠C(已知)
∴______=∠B
AB∥CD(______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com