
【题目】某市为加固长90米,高30米,坝顶宽为6米,迎水坡和背水坡都是1:1的横断面是梯形的防洪大坝,要将大坝加高2米,背水坡坡度改为1:1.5,已知坝顶宽不变,求大坝横戴面积增加多少平方米?
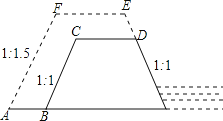
【答案】大坝横戴面积增加392平方米.
【解析】
过C作CG⊥AB于G,过D作DH⊥AB于H,过F作FM⊥AB于M,过E作EN⊥AB于N,求出AQ和BQ的长,根据题意得出增加的面积等于加宽后的梯形面积减去原来的梯形面积,根据梯形的面积公式求出即可.
过C作CG⊥AB于G,过D作DH⊥AB于H,过F作FM⊥AB于M,过E作EN⊥AB于N,
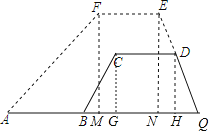
则四边形CDHG和四边形EFMN是矩形,
即CG=DH=30m,FM=EN=30+2=32(m),
∵梯形BCDQ的迎水坡和背水坡的坡度都是1:1,
∴BG=QH=30m,
同理AM=32×1.5=48(m),QN=32m,
∴AQ=48+6+32=86(m),BQ=30+6+30=66(m),
大坝横截面面积增加![]() ×(6+86)×32-
×(6+86)×32-![]() ×(6+66)×30=392(m2),
×(6+66)×30=392(m2),
答:大坝横戴面积增加392平方米.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】选择适当的方法解下列方程:
(1)(x-1)2+2x(x-1)=0;
(2)x2-6x-6=0;
(3)6 000(1-x)2=4 860;
(4)(10+x)(50-x)=800;
(5)(2x-1)2=x(3x+2)-7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.

(1)判断△OBC的形状,并证明你的结论
(2)求BC的长
(3)求⊙O的半径OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
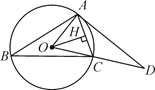
【题目】如图,△ABC内接于⊙O,OH⊥AC于点H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5![]() ,请求出:
,请求出:
(1)∠AOC的度数;
(2)劣弧![]() 的长;(结果保留π)
的长;(结果保留π)
(3)线段AD的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
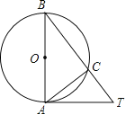
A. AB=4,AT=3,BT=5 B. ∠B=45°,AB=AT
C. ∠B=55°,∠TAC=55° D. ∠ATC=∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,cot∠ADB=![]() ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=![]() ,AC=3.
,AC=3.
(1)求AD的长;
(2)求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com