
【题目】如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=![]() ,AC=3.
,AC=3.
(1)求AD的长;
(2)求图中阴影部分的面积.

科目:初中数学 来源: 题型:
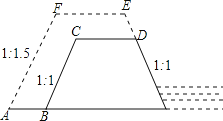
【题目】某市为加固长90米,高30米,坝顶宽为6米,迎水坡和背水坡都是1:1的横断面是梯形的防洪大坝,要将大坝加高2米,背水坡坡度改为1:1.5,已知坝顶宽不变,求大坝横戴面积增加多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
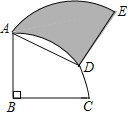
【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(2,4)在其图象上,则(﹣2,4)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的垂线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=x和y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线![]()
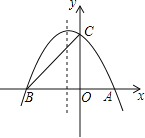
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
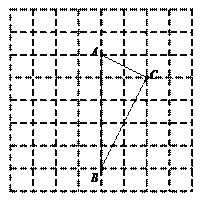
【题目】如图,在由边长为1的小正方形组成的网格图中,有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形.)
(1)△ABC是 三角形(填“锐角”、“直角”或“钝角”);
(2)若P、Q分别为线段AB、BC上的动点,当PC+PQ取得最小值时,
① 在网格中用无刻度的直尺,画出线段PC、PQ.(请保留作图痕迹.)
② 直接写出PC+PQ的最小值: .
查看答案和解析>>
科目:初中数学 来源: 题型:
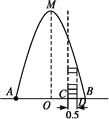
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C处(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4 m,AC=3 m,网球飞行最大高度OM=5 m,圆柱形桶的直径为0.5 m,高为0.3 m(网球的体积和圆柱形桶的厚度忽略不计).
(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.某商场销售一种品牌的小米,进价是40元/袋.市场调查后发现,售价是60元/袋时,平均每星期的销售量是300袋,而销售单价每降低1元,平均每星期就可多售出30袋.
(1)若每袋小米降价x元,写出该商场销售该品牌小米每星期获得的利润w(元)与x(元)之间的函数关系式.
(2)在(1)的条件下,每袋小米的销售单价是多少元时,该商场每星期销售这种品牌小米获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com