
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线![]()
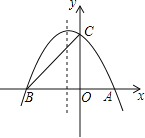
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
【答案】(1)![]()
(2)M点坐标为(0,0)或![]()
【解析】
(1)根据抛物线的对称轴得到抛物线的顶点式,然后代入已知的两点理由待定系数法求解即可。
(2)首先求得点B的坐标,然后分CM=BM时和BC=BM时两种情况根据等腰三角形的性质求得点M的坐标即可。
解:(1)∵抛物线的对称轴是直线![]() ,∴设抛物线的解析式
,∴设抛物线的解析式![]() 。
。
把A(2,0)C(0,3)代入得: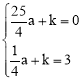 ,解得:
,解得: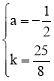 。
。
∴抛物线的解析式为![]() ,即
,即![]() 。
。
(2)由y=0得![]() ,∴x1=1,x2=﹣3。
,∴x1=1,x2=﹣3。
∴B(﹣3,0)。
分两种情况讨论(因为BC=MC时,点M已不在线段AB上,无需考虑):
①CM=BM时,
∵BO=CO=3, 即△BOC是等腰直角三角形,
∴当M点在原点O时,△MBC是等腰三角形。
∴M点坐标(0,0)。
②BC=BM时,
在Rt△BOC中,BO=CO=3,∴由勾股定理得![]() 。
。
∴BM=![]() 。
。
∴M点坐标![]() 。
。
综上所述,当△MBC为等腰三角形时,M点坐标为(0,0)或![]() 。
。
题型】解答题


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凤城中学九年级(3)班的班主任让同学们为班会活动设计一个摸球方案,这些球除颜色外都相同,拟使中奖概率为50%.
(1)小明的设计方案:在一个不透明的盒子中,放入黄、白两种颜色的球共6个,搅匀后从中任意摸出1个球,摸到黄球则表示中奖,否则不中奖.如果小明的设计符合老师要求,则盒子中黄球应有 个,白球应有 个;
(2)小兵的设计方案:在一个不透明的盒子中,放入2个黄球和1个白球,搅匀后从中任意摸出2个球,摸到的2个球都是黄球则表示中奖,否则不中奖,该设计方案是否符合老师的要求?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
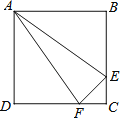
A. 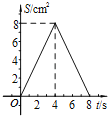 B.
B. 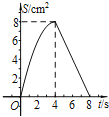
C. 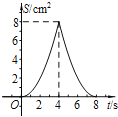 D.
D. 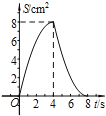
查看答案和解析>>
科目:初中数学 来源: 题型:
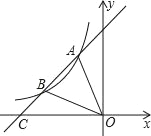
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积.
(3)根据图象回答:当x为何值时,kx+b≥![]() (请直接写出答案) .
(请直接写出答案) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=![]() ,AC=3.
,AC=3.
(1)求AD的长;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
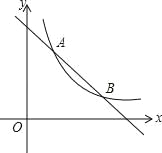
【题目】如图,一次函数 y=﹣x+4 的图象与反比例 y=![]() (k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(1)求点 A、B 的坐标及反比例函数的表达式;
(2)在 x 轴上找一点,使 PA+PB 的值最小,求满足条件的点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板点A位置的变化为A→Al→A2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30°的角,则点A滚到A2位置时共走过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com