
【题目】如图,线段![]() ,动点
,动点![]() 以
以![]() 的速度从
的速度从![]() 在线段
在线段![]() 上运动,到达点
上运动,到达点![]() 后,停止运动;动点
后,停止运动;动点![]() 以
以![]() 的速度从
的速度从![]() 在线段
在线段![]() 上运动,到达点
上运动,到达点![]() 后,停止运动.若动点
后,停止运动.若动点![]() 同时出发,设点
同时出发,设点![]() 的运动时间是
的运动时间是![]() (单位:
(单位:![]() )时,两个动点之间的距离为S(单位:
)时,两个动点之间的距离为S(单位:![]() ),则能表示
),则能表示![]() 与
与![]() 的函数关系的是( )
的函数关系的是( )
![]()
A.  B.
B. 
C. 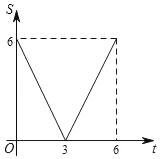 D.
D. 
【答案】D
【解析】
根据题意可以得到点P运动的快,点Q运动的慢,可以算出动点P和Q相遇时用的时间和点Q到达终点时的时间,从而可以解答本题.
:设点Q的运动时间是t(单位:s)时,两个动点之间的距离为s(单位:cm),
6=2t+t,解得:t=2,即t=2时,P、Q相遇,即S=0,.
P到达B点的时间为:6÷2=3s,此时,点Q距离B点为:3,即S=3
P点全程用时为12÷2=6s,Q点全程用时为6÷1=6s,即P、Q同时到达A点
由上可得,刚开始P和Q两点间的距离在越来越小直到相遇时,它们之间的距离变为0,此时用的时间为2s;
相遇后,在第3s时点P到达B点,从相遇到点P到达B点它们的距离在变大,1s后P点从B点返回,点P继续运动,两个动点之间的距离逐渐变小,同时达到A点.
故选:D.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为 cm2 . (结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣3,4),B(﹣5,2),C(﹣2,1).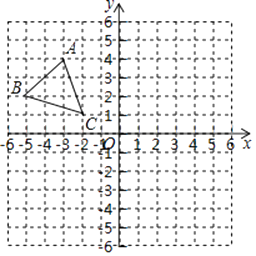
(1)画出△ABC关于y轴对称图形△A1B1C1;
(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;
(3)求(2)中线段OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程|x-1|+|x+2|=5.由绝对值的几何意义知,该方程表示求在数轴上与1和-2的距离之和为5的点对应的x的值.在数轴上,1和-2的距离为3,满足方程的x对应点在1的右边或-2的左边,若x对应点在1的右边,由图可以看出x=2;同理,若x对应点在-2的左边,可得x=-3,故原方程的解是x=2或x=-3.
![]()
参考阅读材料,解答下列问题:
(1)方程|x+3|=4的解为________.
(2)解不等式|x-3|+|x+4|≥9;
(3)若|x-3|+|x+4|≥a对任意的x都成立,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
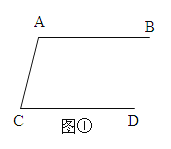
【题目】(1)如图①,AB∥CD,那么∠A+∠C= 度
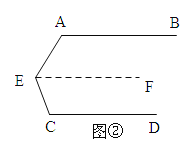
(2)如图②,AB∥CD∥EF,那么∠A+∠AEC+∠C= 度
(3)如图③,AB∥GH∥MN∥CD,那么∠A+∠AGM+∠GMC+∠C=度,并说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com