
 “十•一”黄金周期间,少林寺风景区在7天假期中每天旅游的人数变化如下表( 正数表示比前一天多的人数,负数表示比前一天少的人数):
“十•一”黄金周期间,少林寺风景区在7天假期中每天旅游的人数变化如下表( 正数表示比前一天多的人数,负数表示比前一天少的人数):| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
分析 (1)先计算出5号的游客数,即可得出答案;
(2)分别计算出每天的人数,即可作出判断.
(3)根据(2)中计算出每天的人数可以画出折线图.
解答 解:(1)根据题意得:5日的人数是:5.5+1.6+0.8+0.4-0.5-0.8=6.6(万人);
故答案为:6.6;
(2)设9月30日的游客人数为x万人,由统计表可以看出:
1日的人数是:x+1.6=(x+1.6)万人;
2日的人数是:x+1.6+0.8=(x+2.4)万人;
3日的人数是:x+2.4+0.4=(x+2.8)万人;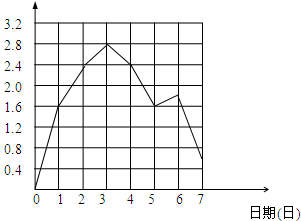
4日的人数是:x+2.8-0.4=(x+2.4)万人;
5日的人数是:x+2.4-0.8=(x+1.6)万人;
6日的人数是:x+1.6+0.4=(x+2)万人;
7日的人数是:x+2-1.2=(x+0.8)万人.
则七天内游客人数最多的是3日;最少的是7日;
故答案为:3,7;
(3)画图如下.
点评 本题考查的是条形统计图和折线统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.折形统计图能清楚地表示出事物的变化情况.


科目:初中数学 来源: 题型:解答题
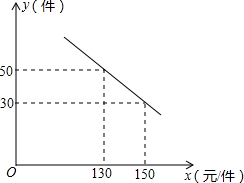 网购的普及标志着我国零售业进入了电商时代.某淘宝网店购进一种成本为100元/件的新商品,在试销中发现:销售单价x(元)与每天销售量y(件)之间满足如图所示的关系.
网购的普及标志着我国零售业进入了电商时代.某淘宝网店购进一种成本为100元/件的新商品,在试销中发现:销售单价x(元)与每天销售量y(件)之间满足如图所示的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,直线AB,CD相交于点O,已知∠AOC=80°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠EOD和∠AOE的度数.
如图所示,直线AB,CD相交于点O,已知∠AOC=80°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠EOD和∠AOE的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在13×13的网格图中,已知△ABC和点M(1,2).
在13×13的网格图中,已知△ABC和点M(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com