
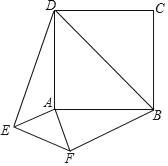
【题目】如图,在边长为3正方形ABCD的外部作Rt△AEF,且AE=AF=1,连接DE,BF,BD,则DE2+BF2=_____.
【答案】20
【解析】
连接BE,DF交于点O,由题意可证△AEB≌△AFD,可得∠AFD=∠AEB,可证∠EOF=90°,由勾股定理可求解.
连接BE,DF交于点O,
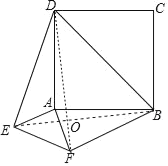
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∵△AEF是等腰直角三角形,
∴AE=AF,∠EAF=90°,
∴∠EAB=∠DAF,
在△AEB和△AFD中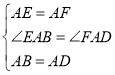 ,
,
∴△AEB≌△AFD(SAS),
∴∠AFD=∠AEB,
∵∠AEF+∠AFE=90°=∠AEB+∠BEF+∠AFE=∠BEF+∠AFE+∠AFD=∠BEF+∠EFD=90°,
∴∠EOF=90°,
∴EO2+FO2=EF2,DO2+BO2=DB2,EO2+DO2=DE2,OF2+BO2=BF2,
∴DE2+BF2=EF2+DB2=2AE2+2AD2=20,
故答案为:20.


科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2﹣3ax+c(a≠0)与y轴交于点C(0,﹣4)与x轴交于点A.B,点A的坐标为(4,0).
(1)求该抛物线的解析式.
(2)点D是线段AB上的动点,过点D作DE∥AC,交BC于点E,连接CD.当△CDE的面积最大时,求点D的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点Q(2,0).问:是否存在这样的直线l,使得△OQF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
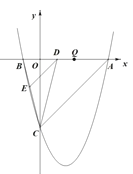
查看答案和解析>>
科目:初中数学 来源: 题型:
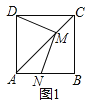
【题目】如图1,点M放在正方形ABCD的对角线AC(不与点A重合)上滑动,连结DM,做MN⊥DM,交直线AB于N.
(1)求证:DM=MN;
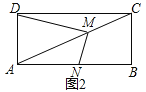
(2)若将(1)中的正方形变为矩形,其余条件不变如图,且DC=2AD,求MD:MN的值;
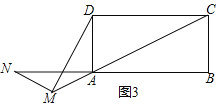
(3)在(2)中,若CD=nAD,当M滑动到CA的延长线上时(如图3),请你直接写出MD:MN的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠BAC=90°,∠BAC 的平分线交 BC 于点 O,以 O 为圆心作圆,⊙O 与 AC 相切于点 D.
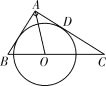
(1)试判断 AB 与⊙O 的位置关系,并加以证明;
(2)在 Rt△ABC 中,若 AC=6,AB=3,求切线 AD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
(1)点A的坐标:_____;点B的坐标:_____;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你将有关内容补充完整.例题:求一元二次方程![]() 的两个解.
的两个解.
(1)解法一:选择合适的一种方法(公式法、配方法、分解因式法)求解.解方程:![]() ;
;
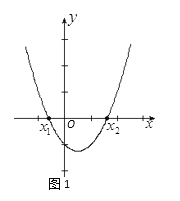
(2)解法二:利用二次函数图象与坐标轴的交点求解,如图1所示,把方程![]() 的解看成是二次函数y= 的图象与x轴交点的横坐标,即x1,x2就是方程的解.
的解看成是二次函数y= 的图象与x轴交点的横坐标,即x1,x2就是方程的解.
(3)解法三:利用两个函数图象的交点求解.
①把方程![]() 的解看成是一个二次函数y= 的图象与一个一次函数y= 的图象交点的横坐标;
的解看成是一个二次函数y= 的图象与一个一次函数y= 的图象交点的横坐标;
②画出这两个函数的图象,用x1,x2在x轴上标出方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
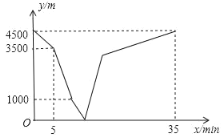
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,∠ADB=∠CDB=∠BAC=45°,结论:①∠ABC=90°,②AB=BC,③AD2+DC2=2AB2,④AD+DC=![]() BD,其中正确的有( )
BD,其中正确的有( )
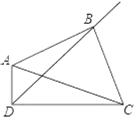
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com