
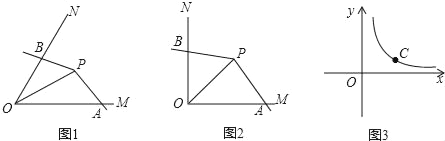
【题目】如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OAOB=OP2,我们就把∠APB叫做∠MON的智慧角.
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.
(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子分别表示∠APB的度数和△AOB的面积.
(3)如图3,C是函数y=![]() (x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
(x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
【答案】(1)证明见解析 (2)∠APB=180°﹣![]() α,S△AOB=2sinα (3)(
α,S△AOB=2sinα (3)(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )
)
【解析】
(1)由角平分线求出∠AOP=∠BOP=![]() ∠MON=45°,再证出∠OAP=∠OPB,证明△AOP∽△POB,得出对应边成比例
∠MON=45°,再证出∠OAP=∠OPB,证明△AOP∽△POB,得出对应边成比例![]() ,得出OP2=OAOB,即可得出结论;
,得出OP2=OAOB,即可得出结论;
(2)由∠APB是∠MON的智慧角,得出![]() ,证出△AOP∽△POB,得出对应角相等∠OAP=∠OPB,即可得出∠APB=180°﹣
,证出△AOP∽△POB,得出对应角相等∠OAP=∠OPB,即可得出∠APB=180°﹣![]() α;过点A作AH⊥OB于H,由三角形的面积公式得出:S△AOB=
α;过点A作AH⊥OB于H,由三角形的面积公式得出:S△AOB=![]() OBAH,即可得出S△AOB=2sinα;
OBAH,即可得出S△AOB=2sinα;
(3)设点C(a,b),则ab=3,过点C作CH⊥OA于H;分两种情况:
①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,BC=2CA不可能;当得A在x轴的正半轴上时;先求出![]() ,由平行线得出△ACH∽△ABO,得出比例式:
,由平行线得出△ACH∽△ABO,得出比例式:![]() ,得出OB=3b,OA=
,得出OB=3b,OA=![]() ,求出OAOB=
,求出OAOB=![]() ,根据∠APB是∠AOB的智慧角,得出OP,即可得出点P的坐标;
,根据∠APB是∠AOB的智慧角,得出OP,即可得出点P的坐标;
②当点B在y轴的负半轴上时;由题意得出:AB=CA,由AAS证明△ACH≌△ABO,得出OB=CH=b,OA=AH=![]() a,得出OAOB=
a,得出OAOB=![]() ,求出OP,即可得出点P的坐标.
,求出OP,即可得出点P的坐标.
(1)证明:∵∠MON=90°,P为∠MON的平分线上一点,
∴∠AOP=∠BOP=![]() ∠MON=45°,
∠MON=45°,
∵∠AOP+∠OAP+∠APO=180°,
∴∠OAP+∠APO=135°,
∵∠APB=135°,
∴∠OAP=∠OPB,
∴△AOP∽△POB,
∴![]() ,
,
∴OP2=OAOB,
∴∠APB是∠MON的智慧角;
(2)解:∵∠APB是∠MON的智慧角,
∴OAOB=OP2,
∴![]() ,
,
∵P为∠MON的平分线上一点,
∴∠AOP=∠BOP=![]() α,
α,
∴△AOP∽△POB,
∴∠OAP=∠OPB,
∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°﹣![]() α,
α,
即∠APB=180°﹣![]() α;
α;
过点A作AH⊥OB于H,连接AB;如图1所示:
则S△AOB=![]() OBAH=
OBAH=![]() OBOAsinα=
OBOAsinα=![]() OP2sinα,
OP2sinα,
∵OP=2,
∴S△AOB=2sinα;
(3)设点C(a,b),则ab=3,过点C作CH⊥OA于H;分两种情况:
①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,如图2所示:
BC=2CA不可能;
当点A在x轴的正半轴上时,如图3所示:
∵BC=2CA,
∴![]() ,
,
∵CH∥OB,
∴△ACH∽△ABO,
∴![]() ,
,
∴OB=3b,OA=![]() ,
,
∴OAOB=![]() ,
,
∵∠APB是∠AOB的智慧角,
∴OP=![]() ,
,
∵∠AOB=90°,OP平分∠AOB,
∴点P的坐标为:(![]() ,
,![]() );
);
②当点B在y轴的负半轴上时,如图4所示:
∵BC=2CA,
∴AB=CA,
在△ACH和△ABO中,
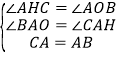 ,
,
∴△ACH≌△ABO(AAS),
∴OB=CH=b,OA=AH=![]() a,
a,
∴OAOB=![]() ab=
ab=![]() ,
,
∵∠APB是∠AOB的智慧角,
∴OP=![]() ,
,
∵∠AOB=90°,OP平分∠AOB,
∴点P的坐标为:(![]() ,﹣
,﹣![]() );
);
综上所述:点P的坐标为:(![]() ,
,![]() ),或(
),或(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
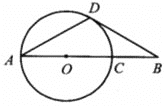
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D在⊙O上,连接AD,BD,∠A=∠B=30°.
证明:(1)BD是⊙O的切线
(2)如果BD=2求OC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )

A. (11﹣2![]() )米 B. (11
)米 B. (11![]() ﹣2
﹣2![]() )米 C. (11﹣2
)米 C. (11﹣2![]() )米 D. (11
)米 D. (11![]() ﹣4)米
﹣4)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,污水处理公司为某楼房建一座周长为30米的三级污水处理池,平面图为矩形![]() ,
,![]() 米,中间两条隔墙分别为
米,中间两条隔墙分别为![]() 、
、![]() ,池墙的厚度不考虑.
,池墙的厚度不考虑.
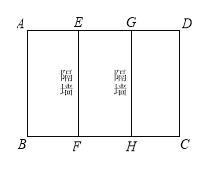
(1)用含![]() 的代数式表示外围墙
的代数式表示外围墙![]() 的长度;
的长度;
(2)如果设计时要求矩形水池![]() 恰好被隔墙分成三个全等的矩形,且它们均与矩形
恰好被隔墙分成三个全等的矩形,且它们均与矩形![]() 相似,求此时
相似,求此时![]() 的长;
的长;
(3)如果设计时要求矩形水池![]() 恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元,中间两条隔墙建造单价每米300元,池底建造的单价为每平方米100元.试计算此项工程的总造价.(结果精确到1元)
恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元,中间两条隔墙建造单价每米300元,池底建造的单价为每平方米100元.试计算此项工程的总造价.(结果精确到1元)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OFDE=OE2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(-1,n),请完成下列任务:
(1)(尝试)
当t=2时,抛物线y=t(x2-3x+2)+(1-t)(-2x+4)的顶点坐标为________;
(2)判断点A是否在抛物线L上;
(3)求n的值.
(4)(发现)
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为________.
(5)(应用)
二次函数y=-3x2+5x+2是二次函数y=x23x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
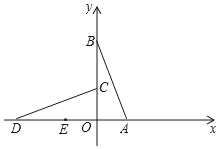
【题目】如图,已知点A(1,0),B(0,3),将△AOB绕点O逆时针旋转90°,得到△COD,设E为AD的中点.
(1)若F为CD上一动点,求出当△DEF与△COD相似时点F的坐标;
(2)过E作x轴的垂线l,在直线l上是否存在一点Q,使∠CQO=∠CDO?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com