
【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
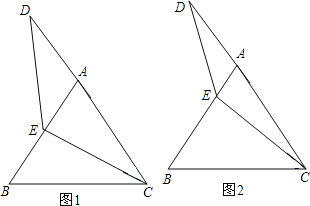
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:AD BE;
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
【答案】(1)AD=BE;(2)证明见解析
【解析】分析:(1)根据题意易得∠D=∠AED=30°,即可得AD=AE,再根据AE=BE,即可解题;
(2)通过作EF∥AC构造等边三角形把BE转化为EF,再利用“角角边”易证△AED≌△FCE,可得AD=FE,即可解题.
本题解析:
(1)AD=BE;
(2)过点E作EF∥AC交BC于点F,
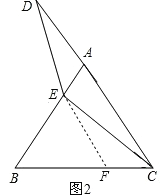
∴∠EFB=∠ACB,∠BEF=∠BAC,∠FEC=∠ECA,
∵△ABC是等边三角形,
∴∠ACB=∠BAC=∠B=60°,
∴∠EFB=∠BEF=∠B=60°,
∴△BEF是等边三角形,
∴BE=EF,
∵ED=EC,
∴∠D=∠ECA,
∴∠D=∠FEC,
∵∠BFE=∠BAC=60°,
∴∠EAD=∠CFE=120°,
在△AED和△FCE中,
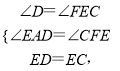
∴△AED≌△FCE(AAS),
∴AD=FE,
∴AD=BE。


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】已知甲同学手中藏有三张分别标有数字![]() 、
、![]() 、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |

A.当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
B.假如你去转动转盘一次,获得铅笔的概率大约是0.70
C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D.转动转盘10次,一定有3次获得文具盒
查看答案和解析>>
科目:初中数学 来源: 题型:
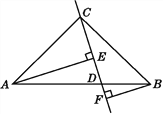
【题目】如图:在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断AC与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.
(1)求证:四边形AECF是菱形;
(2)若AB=4,BC=8,求菱形AECF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com