
【题目】如图,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为弧AN上一点.且弧AC=弧AM,连接CM,交AB于点E,交AN于点F,现给出以下结论:
①AD=BD;②∠MAN=90°;③弧AM =弧BM ;④∠ACM+∠ANM=∠MOB;⑤AE=![]() MF.其中正确结论的序号是_____.
MF.其中正确结论的序号是_____.
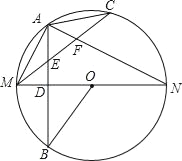
【答案】①②③④⑤
【解析】
根据AB⊥MN和垂径定理得出①③正确;利用MN是直径得出②正确;④,根据等弧所对的圆心角相等及外角的性质可得出④正确;根据等弧所对的圆周角相等得:∠MAE=∠AME,再由等角的余角相等得:∠EAF=∠AFE,可得出⑤正确即可.
∵MN是⊙O的直径,AB⊥MN,
∴AD=BD,![]() ,故①③正确;
,故①③正确;
∵MN是⊙O的直径,
∴∠MAN=90°,
故②正确;
连接OA,
∵![]() ,
,
∴∠AOM=∠BOM=∠ANM+∠OAN,
∵OA=ON,
∴∠OAN=∠ANM,
∴∠MOB=2∠ANM,
∵∠ANM=∠ACM,
∴∠ACM+∠ANM=∠MOB;
故④正确;
∵![]() ,
,
∴∠MAE=∠AME,
∵∠MAE+∠EAF=90°,∠AME+∠AFE=90°,
∴∠EAF=∠AFE,
∴AE=ME,AE=EF,
∴AE=![]() MF,
MF,
故⑤正确.
正确的结论共5个,①②③④⑤.
故答案为:①②③④⑤.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
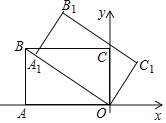
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
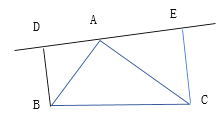
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD![]() DE于点D, CE
DE于点D, CE![]() DE 于点 E.
DE 于点 E.
(1)若BC在DE的同侧(如图所示),且AD=CE,求证:![]()
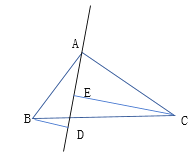
(2)若B、C在的两侧(如图所示 ),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
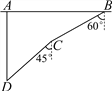
查看答案和解析>>
科目:初中数学 来源: 题型:
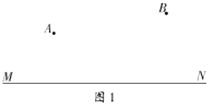
【题目】(1)如图1,要在公路![]() 旁修建一个货物中转站
旁修建一个货物中转站![]() ,分别向
,分别向![]() 、
、![]() 两个开发区运货.若要求货站到
两个开发区运货.若要求货站到![]() 、
、![]() 两个开发区的距离相等,那么货站应建在那里?
两个开发区的距离相等,那么货站应建在那里?
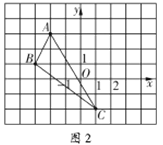
(2)在直角坐标系中,![]() 的三个顶点的位置如图2所示.
的三个顶点的位置如图2所示.
①请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的对应点,不写画法);
的对应点,不写画法);
②直接写出![]() ,
,![]() ,
,![]() 三点的坐标:
三点的坐标:![]() ( ),
( ),![]() ( ),
( ),![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
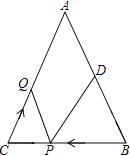
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以每秒2厘米的速度由
上以每秒2厘米的速度由![]() 点向
点向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上以每秒
上以每秒![]() 厘米的速度由
厘米的速度由![]() 点向
点向![]() 点运动,设运动时间为
点运动,设运动时间为![]() (秒)
(秒)![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长度;
的长度;
(2)若点![]() 、
、![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点![]() 、
、![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度
的运动速度![]() 为多少时,能够使
为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
在平面直角坐标系中,任意两点![]() ,
,![]() 之间的位置关系有以下三种情形;
之间的位置关系有以下三种情形;
①如果![]() 轴,则
轴,则![]() ,
,![]()
②如果![]() 轴,则
轴,则![]() ,
,![]()
③如果![]() 与
与![]() 轴、
轴、![]() 轴均不平行,如图,过点
轴均不平行,如图,过点![]() 作与
作与![]() 轴的平行线与过点
轴的平行线与过点![]() 作与
作与![]() 轴的平行线相交于点
轴的平行线相交于点![]() ,则点
,则点![]() 坐标为
坐标为![]() ,由①得
,由①得![]() ;由②得
;由②得![]() ;根据勾股定理可得平面直角坐标系中任意两点的距离公式
;根据勾股定理可得平面直角坐标系中任意两点的距离公式![]()
小试牛刀:
(1)若点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() 则
则![]() ;
;
(2)若点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() 则
则![]() ;
;
(3)若点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() 则
则![]() ;
;
学以致用:
若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴上的动点,当
轴上的动点,当![]() 取得最小值时点
取得最小值时点![]() 的坐标为 并求出
的坐标为 并求出![]() 最小值=
最小值=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com