
【题目】如图,在四边形![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别是
分别是![]() 的中点,
的中点,![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是菱形?请证明你的结论.
是菱形?请证明你的结论.
科目:初中数学 来源: 题型:
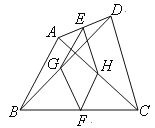
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF

(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
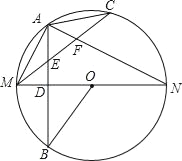
【题目】如图,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为弧AN上一点.且弧AC=弧AM,连接CM,交AB于点E,交AN于点F,现给出以下结论:
①AD=BD;②∠MAN=90°;③弧AM =弧BM ;④∠ACM+∠ANM=∠MOB;⑤AE=![]() MF.其中正确结论的序号是_____.
MF.其中正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
(1)在图中标示出旋转中心P,并写出它的坐标;
(2)以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2,在图中画出△A2B2C2,并写出C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
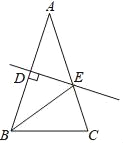
【题目】如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
A. 13B. 16C. 8D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B1C1(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1).
(2)利用方格纸标出△A1B1C1外接圆的圆心P,P点坐标是 ,⊙P的半径= .(保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销的某种商品,每件成本为![]() 元.经市场调研,售价为
元.经市场调研,售价为![]() 元时,可销售
元时,可销售![]() 件;售价每增加
件;售价每增加![]() 元,销售量将减少
元,销售量将减少![]() 件.如果这种商品全部销售完,那么该商店可盈利
件.如果这种商品全部销售完,那么该商店可盈利![]() 元.问:该商店销售了这种商品多少件?每件售价多少元?
元.问:该商店销售了这种商品多少件?每件售价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程2x2+2x﹣1=0的两个根为x1,x2,且x1<x2,下列结论正确的是( )
A. x1+x2=1 B. x1x2=﹣1 C. |x1|<|x2| D. x12+x1=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com