
���� ��1�����ÿ�µ�ʩ��·����x����Ҷ�ÿ�µ�ʩ��·����x������ݡ�ijʩ��·���ܳ�120����ɼס��������̶Ӻ���6������ɣ���֪����2���µĹ�������������3���µĹ��������г������鲢���
��2�����ݷ��ò�����141��Ԫ�г�һԪһ�β���ʽ��⼴�ɣ�
��� �⣺��1�����ÿ�µ�ʩ��·����x����Ҷ�ÿ�µ�ʩ��·����x���
�������$\left\{\begin{array}{l}{2x=3y}\\{6��x+y��=120}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=12}\\{y=8}\end{array}\right.$��
�𣺼�ÿ�µ�ʩ��·����18����Ҷ�ÿ�µ�ʩ��·����12���
��2����������ã�$\left\{\begin{array}{l}{15a+9b��141}\\{12a+8b=120}\end{array}\right.$��
��ã�a��4 b��9��
��a��12��b��12��a��b����������
��9��b��12��a=10-$\frac{2}{3}$b��
��bΪ3�ı�����
��b=9��b=12��
��b=9ʱ��a=4��
��b=12ʱ��a=2
��a=4��b=9��a=2��b=12��
����һ������4���£��Ҷ���9���£�
������������2���£��Ҷ���12���£�
���� ���⿼���˶�Ԫһ�η������Ӧ�ã�����ʱ���ɰ��ܹ�����������1����������Ҫ�����з��̣��飩��Ӧ�����еĹ������⣮�������⣬�ҵ��ؼ�������ҵ����ʵĵ�����ϵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
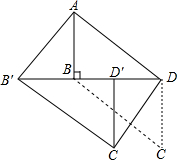 ��ͼ����?ABCD�У�AB��BD��AB=6��AD=3$\sqrt{13}$������BCD��DB�����ƶ�t����λ���õ���B��C��D�䣬����AB�䣬C��D��
��ͼ����?ABCD�У�AB��BD��AB=6��AD=3$\sqrt{13}$������BCD��DB�����ƶ�t����λ���õ���B��C��D�䣬����AB�䣬C��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��4 | B�� | x��4 | C�� | x��4 | D�� | x��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
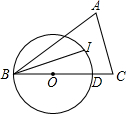 ��ͼ����ABC�У�AC=BC��IΪ��ABC�����ģ�OΪBC��һ�㣬��B��I����ġ�O��BC��D�㣬tan��CBI=$\frac{1}{3}$��AB=6
��ͼ����ABC�У�AC=BC��IΪ��ABC�����ģ�OΪBC��һ�㣬��B��I����ġ�O��BC��D�㣬tan��CBI=$\frac{1}{3}$��AB=6�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����E���߶�AB�ϣ��ֱ���AB��BEΪ�߳���AB���������ȱߡ�ABC�͵ȱߡ�BDE��
��ͼ����E���߶�AB�ϣ��ֱ���AB��BEΪ�߳���AB���������ȱߡ�ABC�͵ȱߡ�BDE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��6 | B�� | 5��-6 | C�� | 1��6 | D�� | 1��-6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com