
分析 (1)根据题目中的信息可以得到1×2+2×3+3×4+…+n×(n+1)的值;
(2)根据(1)中和题目中的信息可以得到1×2×3+2×3×4+3×4×5…+10×11×12-4200的值.
解答 解:(1)∵1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20,
∴1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)(n+2);
(2)1×2×3+2×3×4+3×4×5…+10×11×12-4200
=$\frac{1}{4}×$10×11×12×13-4200=4290-4200=90;
故答案为:(1)$\frac{1}{3}$n(n+1)(n+2);(2)90.
点评 本题考查数字的变化类、有理数的混合运算,解题的关键是明确题意,发现式子中的变化规律.


科目:初中数学 来源: 题型:解答题
| (1)-150+250; | (2)-15+(-23); |
| (3)-5-65; | (4)-26-(-15); |
| (5)-6×(-16); | (6)-$\frac{1}{3}$×27; |
| (7)8÷(-16); | (8)-25÷(-$\frac{2}{3}$); |
| (9)(-0.02)×(-20)×(-5)×4.5; | (10)(-6.5)×(-2)÷(-$\frac{1}{3}$)÷(-5); |
| (11)6+(-$\frac{1}{5}$)-2-(-1.5); | (12)-66×4-(-2.5)÷(-0.1); |
| (13)(-2)2×5-(-2)3÷4; | (14)-(3-5)+32×(1-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
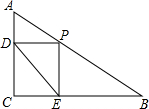 如图,在Rt△ABC中,∠ACB=90°.AC=3,BC=4,P为AB边上一点;且PD⊥AC于D,PE⊥BC于E,则DE的最小值为$\frac{12}{5}$.
如图,在Rt△ABC中,∠ACB=90°.AC=3,BC=4,P为AB边上一点;且PD⊥AC于D,PE⊥BC于E,则DE的最小值为$\frac{12}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com