
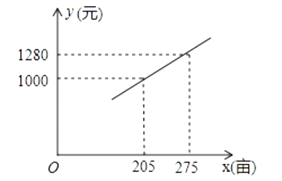
【题目】国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元.种粮大户老王今年种了150亩地,计划明年再承租50~150亩土地种粮以增加收入,考虑各种因素,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示.
(1)今年老王种粮可获得补贴_____________元;
(2)求y与x之间的函数关系式;
(3)若老王明年每亩的售粮收入能达到2100元,设老王明年种粮利润为w(元).(种粮利润=售粮收入-种粮成本+种粮补贴)
①求老王明年种粮利润w(元)与种粮面积x(亩)之间的函数关系式;
②当种粮面积为多少亩时,老王明年种粮利润最高?
【答案】(1)18000;(2)![]() ;(3)①
;(3)①![]() ,②当种粮255亩时,利润最高.
,②当种粮255亩时,利润最高.
【解析】
(1)根据每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,得出老王种粮可获得补贴数目;
(2)利用待定系数法求出一次函数解析式即可;
(3)根据明年每亩的售粮收入能达到2100元,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系为y=4x+180,进而得出W与x的函数关系式,再求二次函数的最值即可解决问题.
(1)∵国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,
∴今年老王种粮可获得补贴120×150=18000元;
故答案为:18000;
(2)假设函数解析式为y=kx+b,根据图象可以得出:图象过(205,1000),(275,1280),
将两点代入解析式得出:
![]() ,
,
解得:
![]() ,
,
则y与x之间的函数关系式为:y=4x+180;
(3)①根据题意得出:
W=(2100-y)x+120x
=[2100-(4x+180)]x+120x
=-4x2+2040x,
②x=-![]()
∵x≥150+50,x≤150+150,
∴200≤x≤300,
∴当x=255,W最大=260100(元).
当种粮面积为255亩时,总收入最高为260100元.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】2020年春节过后受新冠肺炎的疫情影响,在线学习成为同学们学习的重要渠道.我校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
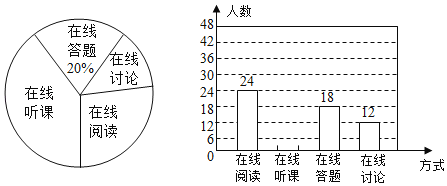
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生900人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字![]() 、
、![]() 、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,将球上的数字记为![]() ,求关于
,求关于![]() 的一元二次方程
的一元二次方程![]() 有实数根的概率;
有实数根的概率;
(2)从中任取一球,将球上的数字作为点的横坐标,记为![]() (不放回);再任取一球,将球上的数字作为点的纵坐标,记为
(不放回);再任取一球,将球上的数字作为点的纵坐标,记为![]() ,试用画树状图(或列表法)表示出点
,试用画树状图(或列表法)表示出点![]() 所有可能出现的结果,并求点
所有可能出现的结果,并求点![]() 落在第二象限内的概率.
落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
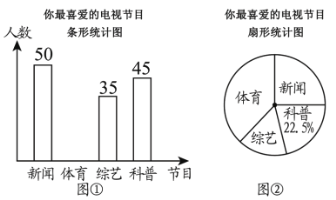
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解八年级500名学生的身体素质情况,体育老师从中随机抽取50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出如下频数分布表和频数分布直方图(不完整):
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 |
|
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
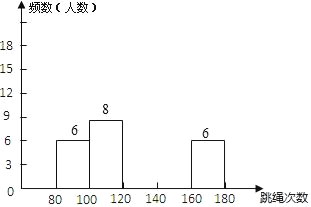
完成下列问题:
(1)请把上面的频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第 组;次数在140≤x<160这组的频率为 ;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120合格,试问该年级合格的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
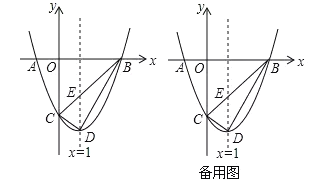
【题目】如图,在平面直角坐标系中,抛物线y=ax2-2x+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、B的坐标分别为(-1,0),(3,0),点D为抛物线的顶点,抛物线的对称轴与直线BC相交于点E.
(1)求抛物线的解析式和点C的坐标;
(2)点P是直线BC下方的抛物线上一动点,当△PBC的面积最大时,请求出P点的坐标和△PBC的最大面积;
(3)点Q是线段BD上的一动点,将△DEQ沿边EQ翻折得到△![]() ,是否存在点Q使得△
,是否存在点Q使得△![]() 与△BEQ的重叠部分图形为直角三角形?若存在,请直接写出BQ的长,若不存在,请说明理由.
与△BEQ的重叠部分图形为直角三角形?若存在,请直接写出BQ的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
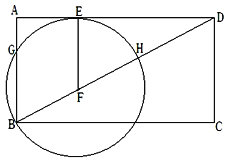
【题目】如图,已知,矩形ABCD中,F是对角线BD上一点,以F为圆心,FB为半径作圆与边AD相切于E,边AB与圆F交于另一点G.
(1)若四边形BGEF是菱形,求证:∠EFD=60o;
(2)若AB=15,AD=36,求AE的长;
(3)若BD与圆F交于另一点H,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com