
【题目】如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是 . 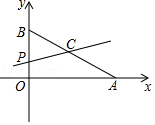
【答案】(0,3)、(4,0)、( ![]() ,0)
,0)
【解析】解:当PC∥OA时,△BPC∽△BOA,
由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(0,3);
当PC∥OB时,△ACP∽△ABO,
由点C是AB的中点,可得P为OA的中点,
此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵∠CAP=∠OAB,
∴Rt△APC∽Rt△ABC,
∴ ![]() =
= ![]() ,
,
∵点A(8,0)和点B(0,6),
∴AB= ![]() =10,
=10,
∵点C是AB的中点,
∴AC=5,
∴ ![]() =
= ![]() ,
,
∴AP= ![]() ,
,
∴OP=OA﹣AP=8﹣ ![]() =
= ![]() ,
,
此时P点坐标为( ![]() ,0),
,0),
综上所述,满足条件的P点坐标为(0,3)、(4,0)、( ![]() ,0).
,0).
故答案为:(0,3)、(4,0)、( ![]() ,0)
,0)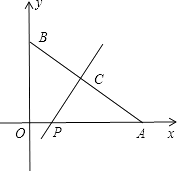
分类讨论:当PC∥OA时,△BPC∽△BOA,易得P点坐标为(0,3);当PC∥OB时,△ACP∽△ABO,易得P点坐标为(4,0);当PC⊥AB时,如图,由于∠CAP=∠OAB,则Rt△APC∽Rt△ABC,计算出AB、AC,则可利用比例式计算出AP,于是可得到OP的长,从而得到P点坐标.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
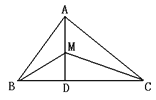
A. 9 B. 35 C. 45 D. 无法计算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90![]() ,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使
,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使![]() DAE=90
DAE=90![]() ,连结CE.
,连结CE.
探究:如图①,当点D在线段BC上时,证明BC=CE+CD.
应用:在探究的条件下,若AB=![]() ,CD=1,则△DCE的周长为_______.
,CD=1,则△DCE的周长为_______.
拓展:(1)如图②,当点D在线段CB的延长线上时,BC、CD、CE之间的数量关系为_______.
(2)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省空间,家里的饭碗一般是摆起来存放的,如果6只饭碗(注:饭碗的大小形状都一样,下同)摆起来的高度为15cm,9只饭碗摆起来的高度为20cm,李老师家的碗橱每格的高度为36cm,则李老师一摞碗最多只能放__只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于每个非零自然数n,抛物线y=x2﹣ ![]() x+
x+ ![]() 与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是( )
与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式![]() 计算出每一行的数据.第一行表示年级,第二行表示班级,第三行表示班级学号的十位数,第四行表示班级学号的个位数.如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的统一学号为_______.
计算出每一行的数据.第一行表示年级,第二行表示班级,第三行表示班级学号的十位数,第四行表示班级学号的个位数.如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的统一学号为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
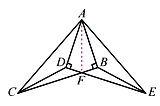
【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宿州市高新区某电子电路板厂到安徽大学从2018年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com