
【题目】对于每个非零自然数n,抛物线y=x2﹣ ![]() x+
x+ ![]() 与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是( )
与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是( )
A.![]()
B.![]()
C.![]()
D.1
【答案】C
【解析】解:令y=x2﹣ ![]() x+
x+ ![]() =0, 即x2﹣
=0, 即x2﹣ ![]() x+
x+ ![]() =0,
=0,
解得x= ![]() 或x=
或x= ![]() ,
,
故抛物线y=x2﹣ ![]() x+
x+ ![]() 与x轴的交点为(
与x轴的交点为( ![]() ,0),(
,0),( ![]() ,0),
,0),
由题意得AnBn= ![]() ﹣
﹣ ![]() ,
,
则A1B1+A2B2+…+A2017B2017=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]() ,
,
故选C.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:

(1)校团委随机调查了多少学生?请你补全条形统计图;
(2)表示“50元”的扇形的圆心角是多少度?被调查的学生每人一周零花钱数额的中位数是多少元?
(3)为捐助贫困山区儿童学习,全校1000名学生每人自发地捐出一周的零花钱.请估算全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得,AC与BD不平行,则AC+BD与AB的大小关系是:AC+BD_____AB.(填“>”“<”或“=”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1 .
②请直接写出AC1 与BD1的位置关系.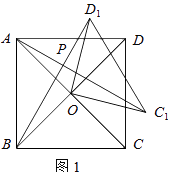
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1 . 判断AC1与BD1的位置关系,说明理由,并求出k的值.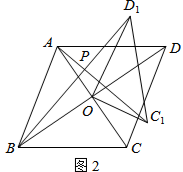
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1 , 设AC1=kBD1 . 请直接写出k的值和AC12+(kDD1)2的值.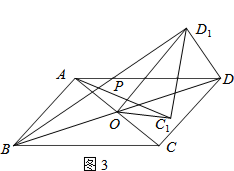
查看答案和解析>>
科目:初中数学 来源: 题型:
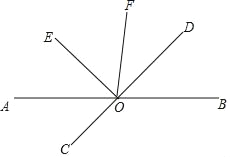
【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=![]() ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是 . 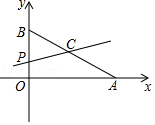
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=4cm,点D是斜边AB的中点,点E从点B出发以1cm/s的速度向点C运动,点F同时从点C出发以一定的速度沿射线CA方向运动,规定:当点E到终点C时停止运动;设运动的时间为x秒,连接DE、DF.
(1)填空:S△ABC= cm2;
(2)当x=1且点F运动的速度也是1cm/s时,求证:DE=DF;
(3)若动点F以3cm/s的速度沿射线CA方向运动;在点E、点F运动过程中,如果有某个时间x,使得△ADF的面积与△BDE的面积存在两倍关系,请你直接写出时间x的值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一个晾衣架的实物图,支架的基本图形是菱形,MN是晾衣架的一个滑槽,点P在滑槽MN上、下移动时,晾衣架可以伸缩,其示意图如图(2)所示,已知每个菱形的边长均为20cm,且AB=CD=CP=DM=20cm. 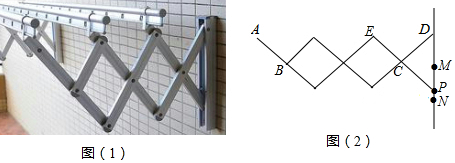
(1)当点P向下滑至点N处时,测得∠DCE=60°时 ①求滑槽MN的长度;
②此时点A到直线DP的距离是多少?
(2)当点P向上滑至点M处时,点A在相对于(1)的情况下向左移动的距离是多少? (结果精确到0.01cm,参考数据 ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com