
ЁОЬтФПЁПдкЫФБпаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌНЋЁїCODШЦЕуOАДФцЪБеыЗНЯђа§зЊЕУЕНЁїC1OD1 ЃЌ а§зЊНЧЮЊІШЃЈ0ЁуЃМІШЃМ90ЁуЃЉЃЌСЌНгAC1ЁЂBD1 ЃЌ AC1гыBD1НЛгкЕуPЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЫФБпаЮABCDЪЧе§ЗНаЮЃЎ
ЂйЧѓжЄЃКЁїAOC1ЁеЁїBOD1 ЃЎ
ЂкЧыжБНгаДГіAC1 гыBD1ЕФЮЛжУЙиЯЕЃЎ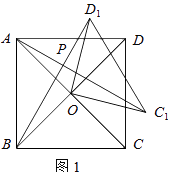
ЃЈ2ЃЉШчЭМ2ЃЌШєЫФБпаЮABCDЪЧСтаЮЃЌAC=5ЃЌBD=7ЃЌЩшAC1=kBD1 ЃЎ ХаЖЯAC1гыBD1ЕФЮЛжУЙиЯЕЃЌЫЕУїРэгЩЃЌВЂЧѓГіkЕФжЕЃЎ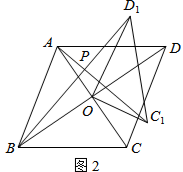
ЃЈ3ЃЉШчЭМ3ЃЌШєЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌAC=5ЃЌBD=10ЃЌСЌНгDD1 ЃЌ ЩшAC1=kBD1 ЃЎ ЧыжБНгаДГіkЕФжЕКЭAC12+ЃЈkDD1ЃЉ2ЕФжЕЃЎ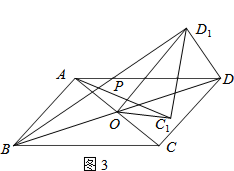
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКжЄУїЃКШчЭМ1ЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрOC=OA=OD=OBЃЌACЁЭBDЃЌ
ЁрЁЯAOB=ЁЯCOD=90ЁуЃЌ
ЁпЁїCODШЦЕуOАДФцЪБеыЗНЯђа§зЊЕУЕНЁїC1OD1ЃЌ
ЁрOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1ЃЌ
ЁрOC1=OD1ЃЌЁЯAOC1=ЁЯBOD1=90Ёу+ЁЯAOD1ЃЌ
дкЁїAOC1КЭЁїBOD1жа
 ЃЌ
ЃЌ
ЁрЁїAOC1ЁеЁїBOD1ЃЈSASЃЉЃЛ
ЂкAC1ЁЭBD1ЃЛ
ЃЈ2ЃЉ
НтЃКAC1ЁЭBD1ЃЎ
РэгЩШчЯТЃКШчЭМ2ЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрOC=OA= ![]() ACЃЌOD=OB=
ACЃЌOD=OB= ![]() BDЃЌACЁЭBDЃЌ
BDЃЌACЁЭBDЃЌ
ЁрЁЯAOB=ЁЯCOD=90ЁуЃЌ
ЁпЁїCODШЦЕуOАДФцЪБеыЗНЯђа§зЊЕУЕНЁїC1OD1ЃЌ
ЁрOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1ЃЌ
ЁрOC1=OAЃЌOD1=OBЃЌЁЯAOC1=ЁЯBOD1ЃЌ
Ёр ![]() ЃЌ
ЃЌ
ЁрЁїAOC1ЁзЁїBOD1ЃЌ
ЁрЁЯOAC1=ЁЯOBD1ЃЌ
гжЁпЁЯAOB=90ЁуЃЌ
ЁрЁЯOAB+ЁЯABP+ЁЯOBD1=90ЁуЃЌ
ЁрЁЯOAB+ЁЯABP+ЁЯOAC1=90ЁуЃЌ
ЁрЁЯAPB=90Ёу
ЁрAC1ЁЭBD1ЃЛ
ЁпЁїAOC1ЁзЁїBOD1ЃЌ
Ёр ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ЃЌ
ЃЌ
Ёрk= ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ
НтЃКШчЭМ3ЃЌгыЃЈ2ЃЉвЛбљПЩжЄУїЁїAOC1ЁзЁїBOD1ЃЌ
Ёр ![]() =
= ![]() =
= ![]() =
= ![]() ЃЌ
ЃЌ
Ёрk= ![]() ЃЛ
ЃЛ
ЁпЁїCODШЦЕуOАДФцЪБеыЗНЯђа§зЊЕУЕНЁїC1OD1ЃЌ
ЁрOD1=ODЃЌ
ЖјOD=OBЃЌ
ЁрOD1=OB=ODЃЌ
ЁрЁїBDD1ЮЊжБНЧШ§НЧаЮЃЌ
дкRtЁїBDD1жаЃЌ
BD12+DD12=BD2=100ЃЌ
ЁрЃЈ2AC1ЃЉ2+DD12=100ЃЌ
ЁрAC12+ЃЈkDD1ЃЉ2=25ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЂйШчЭМ1ЃЌИљОне§ЗНаЮЕФаджЪЕУOC=OA=OD=OBЃЌACЁЭBDЃЌдђЁЯAOB=ЁЯCOD=90ЁуЃЌдйИљОна§зЊЕФаджЪЕУOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1 ЃЌ дђOC1=OD1 ЃЌ РћгУЕШНЧЕФВЙНЧЯрЕШЕУЁЯAOC1=ЁЯBOD1 ЃЌ ШЛКѓИљОнЁАSASЁБПЩжЄУїЁїAOC1ЁеЁїBOD1ЃЛЂкгЩЁЯAOB=90ЁуЃЌдђЁЯOAB+ЁЯABP+ЁЯOBD1=90ЁуЃЌЫљвдЁЯOAB+ЁЯABP+ЁЯOAC1=90ЁуЃЌдђЁЯAPB=90ЁуЫљвдAC1ЁЭBD1ЃЛЃЈ2ЃЉЭМ2ЃЌИљОнСтаЮЕФаджЪЕУOC=OA= ![]() ACЃЌOD=OB=
ACЃЌOD=OB= ![]() BDЃЌACЁЭBDЃЌдђЁЯAOB=ЁЯCOD=90ЁуЃЌдйИљОна§зЊЕФаджЪЕУOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1 ЃЌ дђOC1=OAЃЌOD1=OBЃЌРћгУЕШНЧЕФВЙНЧЯрЕШЕУЁЯAOC1=ЁЯBOD1 ЃЌ МгЩЯ
BDЃЌACЁЭBDЃЌдђЁЯAOB=ЁЯCOD=90ЁуЃЌдйИљОна§зЊЕФаджЪЕУOC1=OCЃЌOD1=ODЃЌЁЯCOC1=ЁЯDOD1 ЃЌ дђOC1=OAЃЌOD1=OBЃЌРћгУЕШНЧЕФВЙНЧЯрЕШЕУЁЯAOC1=ЁЯBOD1 ЃЌ МгЩЯ ![]() ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЕУЕНЁїAOC1ЁзЁїBOD1 ЃЌ ЕУЕНЁЯOAC1=ЁЯOBD1 ЃЌ гЩЁЯAOB=90ЁуЕУЁЯOAB+ЁЯABP+ЁЯOBD1=90ЁуЃЌдђЁЯOAB+ЁЯABP+ЁЯOAC1=90ЁуЃЌдђЁЯAPB=90ЁуЃЌЫљвдAC1ЁЭBD1ЃЛШЛКѓИљОнЯрЫЦБШЕУЕН
ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЕУЕНЁїAOC1ЁзЁїBOD1 ЃЌ ЕУЕНЁЯOAC1=ЁЯOBD1 ЃЌ гЩЁЯAOB=90ЁуЕУЁЯOAB+ЁЯABP+ЁЯOBD1=90ЁуЃЌдђЁЯOAB+ЁЯABP+ЁЯOAC1=90ЁуЃЌдђЁЯAPB=90ЁуЃЌЫљвдAC1ЁЭBD1ЃЛШЛКѓИљОнЯрЫЦБШЕУЕН ![]() =
= ![]() =
= ![]() =
= ![]() ЃЌЫљвдk=
ЃЌЫљвдk= ![]() ЃЛЃЈ3ЃЉгыЃЈ2ЃЉвЛбљПЩжЄУїЁїAOC1ЁзЁїBOD1 ЃЌ дђ
ЃЛЃЈ3ЃЉгыЃЈ2ЃЉвЛбљПЩжЄУїЁїAOC1ЁзЁїBOD1 ЃЌ дђ ![]() =
= ![]() =
= ![]() =
= ![]() ЃЌЫљвдk=
ЃЌЫљвдk= ![]() ЃЛИљОна§зЊЕФаджЪЕУOD1=ODЃЌИљОнЦНааЫФБпаЮЕФаджЪЕУOD=OBЃЌдђOD1=OB=ODЃЌгкЪЧПЩХаЖЯЁїBDD1ЮЊжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэЕУBD12+DD12=BD2=100ЃЌЫљвдЃЈ2AC1ЃЉ2+DD12=100ЃЌгкЪЧгаAC12+ЃЈkDD1ЃЉ2=25ЃЎ
ЃЛИљОна§зЊЕФаджЪЕУOD1=ODЃЌИљОнЦНааЫФБпаЮЕФаджЪЕУOD=OBЃЌдђOD1=OB=ODЃЌгкЪЧПЩХаЖЯЁїBDD1ЮЊжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэЕУBD12+DD12=BD2=100ЃЌЫљвдЃЈ2AC1ЃЉ2+DD12=100ЃЌгкЪЧгаAC12+ЃЈkDD1ЃЉ2=25ЃЎ


 аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌДгЂйЁЯ1ЃНЁЯ2ЃЛЂкЁЯCЃНЁЯDЃЛЂлЁЯAЃНЁЯFШ§ИіЬѕМўжабЁГіСНИізїЮЊвбжЊЬѕМўЃЌСэвЛИізїЮЊНсТлЫљзщГЩЕФУќЬтжаЃЌе§ШЗУќЬтЕФИіЪ§ЮЊ( )

A. 0 B. 1 C. 2 D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
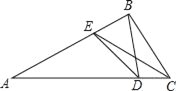
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯABC=100ЁуЃЌЁЯACBЕФЦНЗжЯпНЛABБпгкЕуEЃЌдкACБпШЁЕуDЃЌЪЙЁЯCBD=20ЁуЃЌСЌНгDEЃЌдђЁЯCEDЕФДѓаЁ=_____ЃЈЖШЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯBAC=90![]() ЃЌAB=AC.ЕуDЮЊжБЯпBCЩЯвЛЖЏЕуЃЈЕуDВЛгыЕуBЁЂCжиКЯЃЉЃЌвдADЮЊжБНЧБпдкADгвВрзїЕШбќжБНЧШ§НЧаЮADEЃЌЪЙ
ЃЌAB=AC.ЕуDЮЊжБЯпBCЩЯвЛЖЏЕуЃЈЕуDВЛгыЕуBЁЂCжиКЯЃЉЃЌвдADЮЊжБНЧБпдкADгвВрзїЕШбќжБНЧШ§НЧаЮADEЃЌЪЙ![]() DAE=90
DAE=90![]() ЃЌСЌНсCE.
ЃЌСЌНсCE.
ЬНОПЃКШчЭМЂйЃЌЕБЕуDдкЯпЖЮBCЩЯЪБЃЌжЄУїBC=CE+CD.
гІгУЃКдкЬНОПЕФЬѕМўЯТЃЌШєAB=![]() ЃЌCD=1ЃЌдђЁїDCEЕФжмГЄЮЊ_______.
ЃЌCD=1ЃЌдђЁїDCEЕФжмГЄЮЊ_______.
ЭиеЙЃК(1)ШчЭМЂкЃЌЕБЕуDдкЯпЖЮCBЕФбгГЄЯпЩЯЪБЃЌBCЁЂCDЁЂCEжЎМфЕФЪ§СПЙиЯЕЮЊ_______.
(2)ШчЭМЂлЃЌЕБЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌBCЁЂCDЁЂCEжЎМфЕФЪ§СПЙиЯЕЮЊ_______.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїAOBКЭRtЁїCODжаЃЌЁЯAOB=ЁЯCOD=90ЁуЃЌЁЯB=40ЁуЃЌЁЯC=60ЁуЃЌЕуDдкБпOAЩЯЃЌНЋЭМжаЕФЁїCODШЦЕуOАДУПУы10ЁуЕФЫйЖШбиЫГЪБеыЗНЯђа§зЊвЛжмЃЌдка§зЊЕФЙ§ГЬжаЃЌдкЕк УыЪБЃЌБпCDЧЁКУгыБпABЦНааЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНкЪЁПеМфЃЌМвРяЕФЗЙЭывЛАуЪЧАкЦ№РДДцЗХЕФЃЌШчЙћ6жЛЗЙЭыЃЈзЂЃКЗЙЭыЕФДѓаЁаЮзДЖМвЛбљЃЌЯТЭЌЃЉАкЦ№РДЕФИпЖШЮЊ15cmЃЌ9жЛЗЙЭыАкЦ№РДЕФИпЖШЮЊ20cmЃЌРюРЯЪІМвЕФЭыГїУПИёЕФИпЖШЮЊ36cmЃЌдђРюРЯЪІвЛоћЭызюЖржЛФмЗХ__жЛЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкУПИіЗЧСуздШЛЪ§nЃЌХзЮяЯпy=x2Љ ![]() x+
x+ ![]() гыxжсНЛгкAnЁЂBnСНЕуЃЌвдAnBnБэЪОетСНЕуМфЕФОрРыЃЌдђA1B1+A2B2+Ё+A2017B2017ЕФжЕЪЧЃЈ ЃЉ
гыxжсНЛгкAnЁЂBnСНЕуЃЌвдAnBnБэЪОетСНЕуМфЕФОрРыЃЌдђA1B1+A2B2+Ё+A2017B2017ЕФжЕЪЧЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
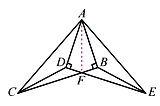
ЁОЬтФПЁПШчЭМЃЌвбжЊRtЁїABCЁеRtЁїADEЃЌЁЯABCЃНЁЯADEЃН90ЁуЃЌBCгыDEЯрНЛгкЕуFЃЌСЌНгCDЃЌEB.
(1)ЭМжаЛЙгаМИЖдШЋЕШШ§НЧаЮЃЌЧыФувЛвЛСаОйЃЛ
(2)ЧѓжЄЃКCFЃНEF.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЪЧвЛЬЈЗХжУдкЫЎЦНзРУцЩЯЕФБЪМЧБОЕчФдЃЌНЋЦфВрУцГщЯѓГЩШчЭМ2ЫљЪОЕФМИКЮЭМаЮЃЌШєЯдЪОЦСЫљдкУцЕФВрБпAOгыМќХЬЫљдкУцЕФВрБпBOГЄОљЮЊ24cmЃЌЕуPЮЊблОІЫљдкЮЛжУЃЌDЮЊAOЕФжаЕуЃЌСЌНгPDЃЌЕБPDЁЭAOЪБЃЌГЦЕуPЮЊЁАзюМбЪгНЧЕуЁБЃЌзїPCЁЭBCЃЌДЙзуCдкOBЕФбгГЄЯпЩЯЃЌЧвBC=12cmЃЎ 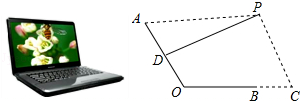
ЃЈ1ЃЉЕБPA=45cmЪБЃЌЧѓPCЕФГЄЃЛ
ЃЈ2ЃЉШєЁЯAOC=120ЁуЪБЃЌЁАзюМбЪгНЧЕуЁБPдкжБЯпPCЩЯЕФЮЛжУЛсЗЂЩњЪВУДБфЛЏЃПДЫЪБPCЕФГЄЪЧЖрЩйЃПЧыЭЈЙ§МЦЫуЫЕУїЃЎЃЈНсЙћОЋШЗЕН0.1cmЃЌПЩгУПЦбЇМЦЫуЦїЃЌВЮПМЪ§ОнЃК ![]() Ёж1.414ЃЌ
Ёж1.414ЃЌ ![]() Ёж1.732ЃЉ
Ёж1.732ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com