【题目】如图，直线y=kx﹣3（k≠0）与坐标轴分别交于点C，B，与双曲线y=﹣
（x＜0）交于点A（m，1），则AB的长是（ ）
A. 2
B. 
C. 2
D. 
科目：初中数学 来源： 题型：
【题目】若将一副三角板按如图所示的方式放置，则下列结论：①
；②如果
，则有
；③如果，则有
；④如果，必有
；其中正确的有( )
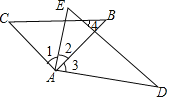
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
“ a 2 ≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式．例如：
x2 4x 5 x2 4x 4 1 x 22 1 ，
∵ x 22 ≥0，
∴ x 22 1 ≥1，
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题：
(1)填空： x2 4x 5 ( x )2＋ ；
(2)已知 x2 4x y2 2y 5 0 ，求 x y 的值；
(3)比较代数式 x2 1与2x 3 的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在社会主义新农村建设中，某乡镇决定对一段公路进行改造，已知这项工程由甲工程队单独做需要40天完成；如果由乙工程先单独做10天，那么剩下的工程还需要两队合做20天才能完成．
（1）求乙工程队单独完成这项工程所需的天数；
（2）求两队合作完成这项工程所需的天数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某日王老师佩戴运动手环进行快走锻炼，两次锻炼后数据如表．与第一次锻炼相比，王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍．设王老师第二次锻炼时平均步长减少的百分率为
．
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注：步数×平均步长＝距离．
(1)根据题意完成表格填空；
(2)求x；
(3)王老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求王老师这500米的平均步长．
查看答案和解析>>
科目：初中数学 来源： 题型：
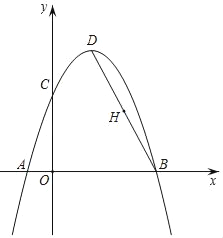
【题目】如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，交y轴于点C，点D为抛物线的顶点，连接BD，点H为BD的中点．请解答下列问题：
（1）求抛物线的解析式及顶点D的坐标；
（2）在y轴上找一点P，使PD+PH的值最小，则PD+PH的最小值为 ．
（注：抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=﹣
，顶点坐标为（﹣，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在菱形ABCD 中，点E，O，F分别是边AB，AC，AD的中点，连接CE、CF、OE、OF．
（1）求证：△BCE≌△DCF；
（2）当AB与BC满足什么条件时，四边形AEOF正方形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知平面直角坐标系中，△ABC的三个顶点的坐标分别为A（2，2），B（1，﹣1），C（3，0）．
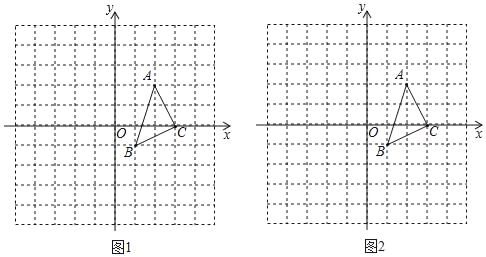
（1）在图1中，画出以点O为位似中心，放大△ABC到原来的2倍的△A1B1C1；
（2）若P（a，b）是AB边上一点，平移△ABC之后，点P的对应点P'的坐标是（a+3，b﹣2），在图2中画出平移后的△A2B2C2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的顶点B、C的坐标分别为(3，4)、(4，2)，且AB平行于x轴，将Rt△ABC向左平移，得到Rt△A′B′C′．若点B′、C′同时落在函数y=
（x＞0）的图象上，则k的值为（ ）
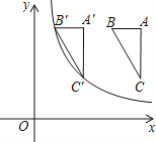
A.2B.4C.6D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
