
【题目】一个铝质的三角形框架的三边长分别为24 cm,30 cm,36 cm,要做一个与它相似的铝质三角形的框架,现有长27 cm,45 cm的两根铝材,要求以其中的一根为边,从另一根上截下两段(允许有余材),则截法有______种.
【答案】1
【解析】
先判断出两根铝材哪根为边,需截哪根,再根据相似三角形的对应边成比例求出另外两边的长,由另外两边的长的和与另一根铝材相比较即可.
∵两根铝材的长分别为27cm,45cm,若45cm为一边时,
则另两边的和为27cm,27<45,不能构成三角形,
∴必须以27cm为一边,45cm的铝材为另外两边,
设另外两边长分别为x,y,则:
若27cm与24cm相对应时,
![]() ,
,
解得:x=33.75cm,y=40.5cm,
x+y=33.75+40.5=74.25cm>45cm,故不成立,
若27cm与36cm相对应时,
![]() ,
,
解得:x=22.5cm,y=18cm,x+y=22.5+18=40.5cm<45cm,成立,
若27cm与30cm相对应时,
![]() ,
,
解得:x=32.4cm,y=21.6cm,x+y=32.4+21.6=54cm>45cm,故不成立,故只有一种截法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 与一次函数y=-2x+m的图象交于A、B两点,AC⊥x轴于C, △AOC的面积为3.
与一次函数y=-2x+m的图象交于A、B两点,AC⊥x轴于C, △AOC的面积为3.
(1)根据这些条件,试确定反比例函数的解析式;
(2)根据这些条件,你能求出一次函数的关系式吗?如果能请你求出来;如果不能,请你添加一个条件,求出一次函数的关系式.(注意:不能添加m的值);
(3)根据你所求出的一次函数的关系式,求出△AOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 经过点
经过点![]() 和点
和点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() ,则:①
,则:①![]() ;②无论
;②无论![]() 取何值,此二次函数图象与
取何值,此二次函数图象与![]() 轴必有两个交点,函数图象截
轴必有两个交点,函数图象截![]() 轴所得的线段长度必大于
轴所得的线段长度必大于![]() ;③当函数在
;③当函数在![]() 时,
时,![]() 随
随![]() 的增大而减小;④当
的增大而减小;④当![]() 时,
时,![]() ;⑤若
;⑤若![]() ,则
,则![]() .以上说法正确的有( )
.以上说法正确的有( )
A. ①②③④⑤ B. ①②④⑤ C. ②③④ D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )

A. 1对 B. 2对 C. 3对 D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 有公共顶点
有公共顶点![]() (顶点均按逆时针排列),
(顶点均按逆时针排列),![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
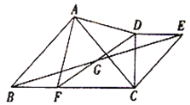
(1)如图,当![]() 时,
时,
求证:①![]() ;
;
②![]() 是等腰直角三角形.
是等腰直角三角形.
(2)当![]() 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出![]() 是何种特殊三角形.
是何种特殊三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com