练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

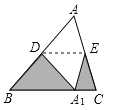
    【题目】如图，三角形ABC的面积为1，将三角形ABC沿着过AB的中点D的直线折叠，使点A落在BC边上的处，折痕为DE，若此时点E是AC的中点，则图中阴影部分的面积为______________．

    【答案】

    【解析】

    作DF⊥BC于点F. 又D、E分别是AB、AC的中点，DE是三角形的中位线，从而DE∥BC，DE=BC，进而可求S△A1BD+S△A1CE=2 S△A1DE，由折叠得：△ADE≌△A1DE，从而可求得结论．

    作DF⊥BC于点F.

    ∵D、E分别是AB、AC的中点，

    ∴DE是△ABC的中位线，

    ∴DE∥BC，DE=BC，

    ∵S△A1BD+S△A1CE=

    =,

    =,

    ∴ S△A1BD+S△A1CE=2 S△A1DE,

    由折叠得：△ADE≌△A1DE，

    ∴S△ADE+S△A1DE=S△ABC，

    ∴S阴影═S△ABC=，

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,已知点A(2,4)、B(4,1)、C(2,0).将三角形ABC向右平移2个单位长度后,再向下平移3个单位长度,得到三角形ABC,其中点A、B、C分别是点A. B. C的对应点。

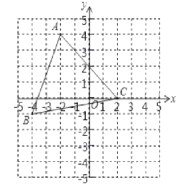
    (1)请在图中画出三角形ABC,并写出点A、B、C的坐标；

    (2)连接AA、BB,求四边形AABB的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校七年级八个级共有320名学生，男女生人数大致相同，调查小组为调查学生的体质健康水平，开展了一次调查研究，请将下面的过程补全:

    收集数据

    (1)调查小组计划选取40名学生的体质健康测试成绩作为样本，下面的取样方法中，合理的是_______(填字母);

    A.抽取七年级1班、2班各20名学生的体质健康测试成绩组成样本

    B.抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本

    C.从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本

    整理、描述数据

    抽样方法确定后，调查小组获得了40名学生的体质健康测试成绩如下:

    整理数据，如下表所示:

    2019年七年级部分学生的体质健康测试成绩统计表

    (2)表格中a=______,b=______;

    分析数据、得出结论

    调查小组将统计后的数据绘制成直方图如图所示:

    (3)若规定80分以上(包括80分)为合格健康体质，从合格率的角度看，这两年的哪年体质测试成绩好?说明理由;

    (4)体育老师计划根据2019年的统计数据安排75分以下的同学参加体质加强训练项目，求全年级约有多少名同学参加此项目.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某文具店准备购进甲、乙两种文具袋，已知甲文具袋每个的进价比乙每个进价多2元，经了解，用120元购进的甲文具袋与用90元购进的乙文具袋的数量相等．

    （1）分别求甲、乙两种文具袋每个的进价是多少元？

    （2）若该文具店用1200元全部购进甲、乙两种文具袋，设购进甲x个，乙y个．

    ①求y关于x的关系式．

    ②甲每个的售价为10元，乙每个的售价为9元，且在进货时，甲的购进数量不少于60个，若这批文具袋全部售完可获利w元，求w关于x的关系式，并说明如何进货该文具店所获利润最大，最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：

    ①2a+b=0；

    ②当﹣1≤x≤3时，y＜0；

    ③若（x1，y1）、（x2，y2）在函数图象上，当x1＜x2时，y1＜y2

    ④9a+3b+c=0

    其中正确的是（　　）

    A. ①②④ B. ①②③ C. ①④ D. ③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB=110°，∠BOC=α，△BOC≌△ADC，∠OCD=60°，连接OD．

    （1）求证：△OCD是等边三角形．

    （2）当α=150°时，试判断△AOD的形状（按角分类），并说明理由．

    （3）求∠OAD的度数．

    （4）探究：当α=　 　时，△AOD是等腰三角形．（不必说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90，∠A=60，CD是斜边AB上的高，若AD=3cm，则斜边AB的长为（ ）

    A.3cmB.6cmC.9cmD.12cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

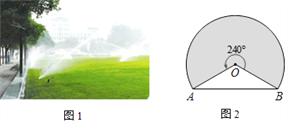
    【题目】如图1是某公园一块草坪上的自动旋转喷水装置，这种旋转喷水装置的旋转角度为240°，它的喷灌区是一个扇形．小涛同学想了解这种装置能够喷灌的草坪面积，他测量出了相关数据，并画出了示意图．如图2，A，B两点的距离为18米，求这种装置能够喷灌的草坪面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某广告公司设计一幅周长为16米的矩形广告牌，广告设计费为每平方米2000元．设矩形一边长为x，面积为S平方米．

    （1）求S与x之间的函数关系式，并写出自变量x的取值范围；

    （2）设计费能达到24000元吗？为什么？

    （3）当x是多少米时，设计费最多？最多是多少元？

    查看答案和解析>>

    同步练习册答案