
【题目】某文具店准备购进甲、乙两种文具袋,已知甲文具袋每个的进价比乙每个进价多2元,经了解,用120元购进的甲文具袋与用90元购进的乙文具袋的数量相等.
(1)分别求甲、乙两种文具袋每个的进价是多少元?
(2)若该文具店用1200元全部购进甲、乙两种文具袋,设购进甲x个,乙y个.
①求y关于x的关系式.
②甲每个的售价为10元,乙每个的售价为9元,且在进货时,甲的购进数量不少于60个,若这批文具袋全部售完可获利w元,求w关于x的关系式,并说明如何进货该文具店所获利润最大,最大利润是多少?
【答案】(1)乙文件袋每个进价为6元,则甲文件袋每个为8元;(2)①![]() ;②w=﹣2x+600,甲文具袋进60个,乙文件袋进120个,获得利润最大为480元.
;②w=﹣2x+600,甲文具袋进60个,乙文件袋进120个,获得利润最大为480元.
【解析】
(1)关键语是“用120元购进的甲文具袋与用90元购进的乙文具袋的数量相等”可根据此列出方程.
(2)①根据题意再由(1)可列出方程
②根据甲每个的售价为10元,乙每个的售价为9元,且在进货时,甲的购进数量不少于60个,若这批文具袋全部售完可获利w元,可列出方程,求出解析式再根据函数图象,分析x的取值即可解答
解:(1)设乙文件袋每个进价为x元,则甲文件袋每个为(x+2)元,
根据题意得:![]()
解得x=6
经检验,x=6是原分式方程的解
∴x+2=8
答:乙文件袋每个进价为6元,则甲文件袋每个为8元
(2)①根据题意得:8x+6y=1200
y=200﹣![]()
②w=(10﹣8)x+(9﹣6)y=2x+3(200﹣![]() )=﹣2x+600
)=﹣2x+600
∵k=﹣2<0
∴w随x的增大而减小
∵x≥60,且为整数
∴当x=60时,w有最大值为,w=60×(﹣2)+600=480
此时,y=200﹣![]() ×60=120
×60=120
答:甲文具袋进60个,乙文件袋进120个,获得利润最大为480元.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价80元,乙种每件进价60元,计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?
(2)服装店在销售中发现:甲服装平均每天可售出20件,每件盈利40元.经市场调查发现:如果每件甲服装降价4元,那么平均每天就可多售出8件,要想平均每天销售甲服装上盈利1200元,那么每件甲服装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() .
.

(1)如图1,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,求线段
,求线段![]() 的长.
的长.
(2)如图2,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边向上构造等边三角形
为边向上构造等边三角形![]() ,线段
,线段![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.连接
的中点.连接![]() ,
,![]() 判断
判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(3)在(2)的条件下,若![]() ,请你直接写出
,请你直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)完成下面的证明.
如图,在四边形![]() 中,
中,![]() ,
,![]() 是
是![]() 的平分线.求证:
的平分线.求证:![]() .
.

证明:![]() 是
是![]() 的平分线(已知)
的平分线(已知)
![]() _________
_________![]() _________(角平分线的定义)
_________(角平分线的定义)
又![]() (已知)
(已知)
![]() _________
_________![]() _________(等量代换)
_________(等量代换)
![]() (____________________________)
(____________________________)
(2)已知线段![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 在直线
在直线![]() 上,且
上,且![]() ,画图并计算
,画图并计算![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC的面积为1,将三角形ABC沿着过AB的中点D的直线折叠,使点A落在BC边上的![]() 处,折痕为DE,若此时点E是AC的中点,则图中阴影部分的面积为______________.
处,折痕为DE,若此时点E是AC的中点,则图中阴影部分的面积为______________.
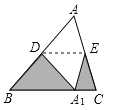
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,将
,将![]() 沿
沿![]() 所在直线折叠,得到
所在直线折叠,得到![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,当四边形
,当四边形![]() 是正方形时,
是正方形时,![]() 等于多少?
等于多少?
(3)若![]() ,
,![]() ,
,![]() 是
是![]() 边上的动点,
边上的动点,![]() 是
是![]() 边上的动点,那么
边上的动点,那么![]() 的最小值是多少?
的最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com