
【题目】如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长.

【答案】(1)作图见解析,⊙P′与直线MN相交;(2)PN=![]() .
.
【解析】分析:在平面直角坐标系中,易知点P′的坐标为(3,2),⊙P′的半径和⊙P的半径相等为3,这样⊙P′就被确定,因为点N在直线MN上,直线MN过(5,0)点且平行于y轴,直线PP′⊥MN,这样利用勾股定理就可求得PN的长度.
解:(1)如图,⊙P′的圆心为(3,2),半径为3,与直线MN相交.

(2)连接PP′,交直线MN于点A,
∵点P、P′的纵坐标相同,∴PP′∥x轴,
又∵MN∥y轴,∴PP′⊥MN,
∴点A的坐标为(5,2).
在Rt△P′NA中,P′N=3,P′A=5-3=2.
∴AN=![]() =
=![]() =
=![]() ,
,
在Rt△PAN中,PA=5-(-3)=8,AN=![]() ,
,
∴PN=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某文具店准备购进甲、乙两种文具袋,已知甲文具袋每个的进价比乙每个进价多2元,经了解,用120元购进的甲文具袋与用90元购进的乙文具袋的数量相等.
(1)分别求甲、乙两种文具袋每个的进价是多少元?
(2)若该文具店用1200元全部购进甲、乙两种文具袋,设购进甲x个,乙y个.
①求y关于x的关系式.
②甲每个的售价为10元,乙每个的售价为9元,且在进货时,甲的购进数量不少于60个,若这批文具袋全部售完可获利w元,求w关于x的关系式,并说明如何进货该文具店所获利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形.
(2)当α=150°时,试判断△AOD的形状(按角分类),并说明理由.
(3)求∠OAD的度数.
(4)探究:当α= 时,△AOD是等腰三角形.(不必说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90,∠A=60,CD是斜边AB上的高,若AD=3cm,则斜边AB的长为( )

A.3cmB.6cmC.9cmD.12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上,过点C作直线![]() ,点D在点C的左边。
,点D在点C的左边。
(1)若BD平分∠ABC,![]() ,则
,则![]() _____°;
_____°;
(2)如图②,若![]() ,作∠CBA的平分线交OC于E,交AC于F,试说明
,作∠CBA的平分线交OC于E,交AC于F,试说明![]() ;
;
(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H.在点B运动过程中![]() 的值是否变化?若不变,求出其值;若变化,求出变化范围.
的值是否变化?若不变,求出其值;若变化,求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
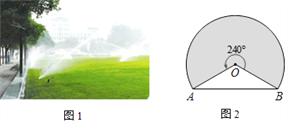
【题目】如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com