
����Ŀ����ͼ��ֱ��y1=�� ![]() x+2��x�ᣬy��ֱ���B��C��������y=ax2+bx+c��a��0��������A��B��C����A����Ϊ����1��0����
x+2��x�ᣬy��ֱ���B��C��������y=ax2+bx+c��a��0��������A��B��C����A����Ϊ����1��0����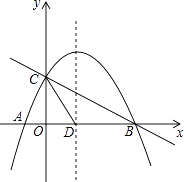
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ�����x�ύ�ڵ�D������CD����P��ֱ��BC�Ϸ��������ϵ�һ���㣨����B��C�غϣ�������P�˶����δ�ʱ���ı���PCDB�������������ʱ�ı���PCDB��������ֵ�͵�P���ꣻ
��3�����������ϵĶԳ������Ƿ����һ��Q��ʹ��QCD����CDΪ���ĵ��������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��x=0���ɵ�y=2��
��y=0���ɵ�x=4��
����B��4��0����C��0��2����
����κ����Ľ���ʽΪy=ax2+bx+c��
����A��B��C������������ʽ�ã�
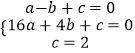 ��
��
��ã� 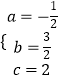 ��
��
���ö��κ����Ĺ�ϵʽΪy=�� ![]() x2+
x2+ ![]() x+2��
x+2��
��2��
�⣺��ͼ1������P��PN��x���ڵ�N����BC�ڵ�M������C��CE��PN��E��
��M��a���� ![]() a+2����P��a����
a+2����P��a���� ![]() a2+
a2+ ![]() a+2����
a+2����
��PM=�� ![]() a2+
a2+ ![]() a+2������
a+2������ ![]() a+2��=��
a+2��=�� ![]() a2+2a��0��x��4����
a2+2a��0��x��4����
��y=�� ![]() x2+
x2+ ![]() x+2=��
x+2=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
���D���������� ![]() ��0����
��0����
��S�ı���PCDB=S��BCD+S��CPM+S��PMB= ![]() BDOC+
BDOC+ ![]() PMCE+
PMCE+ ![]() PMBN��
PMBN��
= ![]() +
+ ![]() a����
a���� ![]() a2+2a��+
a2+2a��+ ![]() ��4��a������
��4��a������
=��a2+4a+ ![]() ��0��x��4����
��0��x��4����
=����a��2��2+ ![]()
��a=2ʱ��S�ı���PCDB��������= ![]() ��
��
�ੁ ![]() a2+
a2+ ![]() a+2=��
a+2=�� ![]() ��22+
��22+ ![]() ��2+2=3��
��2+2=3��
���P��������2��3����
�൱��P�˶�����2��3��ʱ���ı���PCDB�����������ֵΪ ![]() ��
��
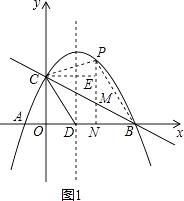
��3��
�⣺��ͼ2���������ߵĶԳ�����x= ![]() ��
��
��OD= ![]() ��
��
��C��0��2����
��OC=2��
��Rt��OCD�У��ɹ��ɶ�������
CD= ![]() ��
��
�ߡ�CDQ����CDΪ���ĵ��������Σ�
��CQ1=DQ2=DQ3=CD��
��ͼ2��ʾ����CE�ͶԳ�����E��
��EQ1=ED=2��
��DQ1=4��
��Q1�� ![]() ��4����Q2��
��4����Q2�� ![]() ��
�� ![]() ����Q3��
����Q3�� ![]() ����
���� ![]() ����
����
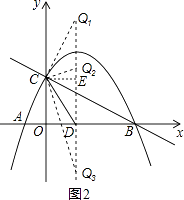
����������1���ֱ������ʽy=�� ![]() x+2��x=0��y=0�������B����C�����ꣻ����κ����Ľ���ʽΪy=ax2+bx+c������A��B��C������������ʽ�����a��b��c��ֵ��������ý���ʽ����2�����M�������Ϊ��a����
x+2��x=0��y=0�������B����C�����ꣻ����κ����Ľ���ʽΪy=ax2+bx+c������A��B��C������������ʽ�����a��b��c��ֵ��������ý���ʽ����2�����M�������Ϊ��a���� ![]() a+2�����Ϳ��Ա�ʾ��P�����꣬���ı���PCDB�����=S��BCD+S��CPM+S��PMB���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ���3���ɣ�2���Ľ���ʽ����������꣬���ɹ��ɶ������CD��ֵ�����Ե�CΪԲ�ģ�CDΪ�뾶�������Գ�����Q1 �� �Ե�DΪԲ��CDΪ�뾶��Բ���Գ����ڵ�Q2 �� Q3 �� ��CE��ֱ�ڶԳ������E���ɵ��������ε����ʼ����ɶ����Ϳ���������ۣ�
a+2�����Ϳ��Ա�ʾ��P�����꣬���ı���PCDB�����=S��BCD+S��CPM+S��PMB���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ���3���ɣ�2���Ľ���ʽ����������꣬���ɹ��ɶ������CD��ֵ�����Ե�CΪԲ�ģ�CDΪ�뾶�������Գ�����Q1 �� �Ե�DΪԲ��CDΪ�뾶��Բ���Գ����ڵ�Q2 �� Q3 �� ��CE��ֱ�ڶԳ������E���ɵ��������ε����ʼ����ɶ����Ϳ���������ۣ�
�����㾫�������ö��κ�����ͼ�����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ȫ��ͬ��������ֽƬABC��DEC�غϷ��ã�������C=900����B=��E=300.
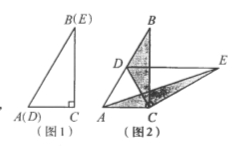


��1������������ͼ2���̶���ABC��ʹ��DEC�Ƶ�C��ת������Dǡ������BC����ʱ����գ��߶�DE��AC��λ�ù�ϵ�� ��
�� ����BDC�����ΪS1����AEC�����ΪS2����S1��S2��������ϵ�� ��
��2��������֤
����DEC�Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����S1��S2��������ϵ��Ȼ�����������Էֱ���������BDC����AEC��BC��CE���ϵĸߣ�����֤��С���IJ��롣
��3����չ̽��
��֪��ABC=600����D�����ƽ������һ�㣬BD=CD=4��OE��AB��BC�ڵ�E����ͼ4������������BA�ϴ��ڵ�F��ʹS��DCF =S��BDC,��ֱ��д����Ӧ��BF�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ����ཻ������ԭ�㣬��A������Ϊ��a��2������B������Ϊ����1���� ![]() ������C������Ϊ��2
������C������Ϊ��2 ![]() ��c������ôa��c��ֵ�ֱ��ǣ� ��
��c������ôa��c��ֵ�ֱ��ǣ� �� 
A.a=��1��c=�� ![]()
B.a=��2 ![]() ��c=��2
��c=��2
C.a=1��c= ![]()
D.a=2 ![]() ��c=2
��c=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ����ABC�У���BAC=90![]() ��AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE=AF����AM��EF����AF=DF����DF=DN��������ȷ�Ľ����У�������
��AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE=AF����AM��EF����AF=DF����DF=DN��������ȷ�Ľ����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬AD��ֱ�ھ�����C��ֱ��DE������Ϊ��D��ACƽ�֡�DAB��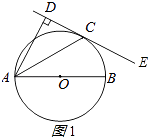
��1����֤��ֱ��DE�ǡ�O�����ߣ�
��2������BC�����룺��ECB���CAB��������ϵ����֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���k2x2��2��k+1��x+1=0������ʵ������
��1����k��ȡֵ��Χ��
��2����k=1ʱ�����������̵��������ֱ�Ϊx1��x2 �� �� ![]() +
+ ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�ڽ��ڡ�O����D��OC���ӳ����ϣ�sinB= ![]() ����CAD=30�㣮
����CAD=30�㣮
��1����֤��AD�ǡ�O�����ߣ�
��2����OD��AB��BC=5����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҽҩ�о���������һ����ҩ��������ҩЧʱ���֣�������˰��涨�������ã���ô��ҩ��2СʱʱѪҺ�к�ҩ����ߣ���ÿ����8�ˣ�1000��=1���ˣ���������˥����10СʱʱѪҺ�к�ҩ��Ϊÿ����4�ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ�����ʱ��x��Сʱ���ı仯��ͼ��ʾ�������˰��涨������ҩ��
��1����y��x֮��Ľ���ʽ��
��2�����ÿ����ѪҺ�к�ҩ��������3�˻�3������ʱ�������Ƽ���ʱ����Ч�ģ���ô�����Чʱ���Ƕ���Сʱ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��l2��l3 �� һ����ֱ��������ABC����������A��B��C�ֱ���l1 �� l2 �� l3�ϣ���ACB=90�㣬AC��l2�ڵ�D����֪l1��l2�ľ���Ϊ1��l2��l3�ľ���Ϊ3���� ![]() ��ֵΪ�� ��
��ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com