练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，AB=AD=DC，∠B=60°，则∠C的度数为(     )

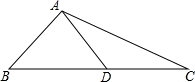
    A．60°   B．30°    C．35°   D．40°


    B【考点】等腰三角形的性质．

    【分析】先根据等腰三角形的性质求出∠ADB的度数，再由平角的定义得出∠ADC的度数，根据等腰三角形的性质即可得出结论．

    【解答】解：∵△ABD中，AB=AD，∠B=60°，

    ∴∠B=∠ADB=60°，

    ∴∠ADC=180°﹣∠ADB=120°，

    ∵AD=CD，

    ∴∠C=（180°﹣∠ADC）÷2=（180°﹣120°）÷2=30°，

    故选：B．

    【点评】本题考查的是等腰三角形的性质，熟知等腰三角形的两底角相等是解答此题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列各点中，在直线y=-4x+1上的点是

    A.（-4，-17） B. （-6）             C. （-1）      D. （1，-5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图,菱形ABCD中,AB=AC=2㎝,求∠BCD的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    8个数的平均数是12，4个数的平均为18，则这12个数的平均数为___________ .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为了倡导“节约用水，从我做起”，市政府决定对市直机关500户家庭的用水情况做一次调查，市政府调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）并将调查结果制成了如图所示的条形统计图。

    （1）       请将条形统计图补充完整；

    （2）       求这100个样本数据的平均数，众数和中位数；

    （3）       根据样本数据，估计市直机关500户家庭中平均用水量不超过12吨的约有多少户？

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，M为等边△ABC内部的一点，且MA=8，MB=10，MC=6，将△BMC绕点C顺时针旋转得到△ANC．下列说法中：①MC=NC；②AM=AN；③S四边形AMCN=S△ABC﹣S△ABM；④∠AMC=120°．正确的有__________．（请填上番号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知0≤x≤，那么函数y=﹣2x2+8x﹣6的最大值是（　　）

    A．﹣10.5      B．2       C．﹣2.5       D．﹣6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．

    （1）求证：AB=AC；

    （2）求证：DE为⊙O的切线；

    （3）若⊙O的半径为5，∠BAC=60°，求DE的长．

    　

    查看答案和解析>>

    同步练习册答案