
【题目】已知:如图所示,O为数轴的原点,A,B分别为数轴上的两点,A点对应的数为﹣30,B点对应的数为100.
(1)A、B的中点C对应的数是 ;
(2)若点D数轴上A、B之间的点,D到B的距离是D到A的距离的3倍,求D对应的数.(提示:数轴上右边的点对应的数减去左边对应的数等于这两点间的距离);
(3)若P点和Q点是数轴上的两个动点,当P点从B点出发,以6个单位长度/秒的速度向左运动时,Q点也从A点出发,以4个单位长度/秒的速度向右运动,设两点在数轴上的E点处相遇,那么E点对应的数是多少?
![]()
【答案】(1)35;(2)点D对应的数是2.5;(3)E点对应的数是22.
【解析】
(1)先计算线段AB的长,再确定中点C,根据数轴得到点C表示的数是多少;
(2)设点D对应的数是x,根据线段DB、DA间关系,得方程求解即可;
(3)根据:点P运动的距离+点Q运算的距离=AB,先求出相遇时间,再求相遇点E表示的数是多少.
解:(1)点A表示的数是﹣30,点B表示的数是100,
所以AB=100﹣(﹣30)=130
因为点C是AB的中点,
∴AC=BC=![]() =65
=65
A、B的中点C对应的数是100﹣65=35.
故答案为:35.
(2)设点D对应的数是x,则由题意,
得100﹣x=3[x﹣(﹣30)]
解得,x=2.5
所以点D对应的数是2.5.
(3)设t秒后相遇,
由题意,4t+6t=130,
解得,t=13,
BE=100﹣6t=78,
100﹣78=22
答:E点对应的数是22.
故答案为:(1)35;(2)点D对应的数是2.5;(3)E点对应的数是22.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2),

(1)请画出△ABC向左平移1个单位长度,再向上平移2个单位长度后的△A′B′C′,(其中A′、B′、C′分别是A、B、C的对应点)
(2)直接写出A′、B′、C′三点的坐标:A′(_____,______);B′(_____,______);C′(_____,______).
(3)△ABC的面积为______________平方单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
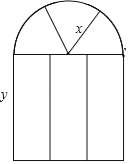
【题目】某窗户的形状如图所示(图中长度单位:cm),其中上部是半径为xcm的半圆形,下部是宽为ycm的长方形.
(1)用含x,y的式子表示窗户的面积S;
(2)当x=40,y=120时,求窗户的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )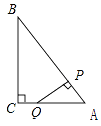
A.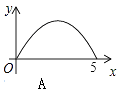
B.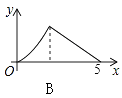
C.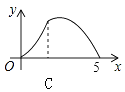
D.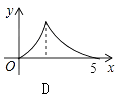
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=![]() (AC﹣AB);
(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF之间的数量关系。
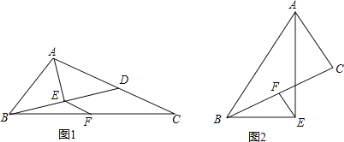
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD 中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图2)中补全他的证明思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
(1)证明:四边形CFAE为菱形;
(2)连接EF交AC于点O,若BC=10,求线段OF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com