
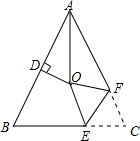
 如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )
如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )| A. | 50° | B. | 45° | C. | 65° | D. | 30° |
分析 连接OB、OC,根据角平分线的定义求出∠BAO,根据等腰三角形两底角相等求出∠ABC,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB,根据等边对等角可得∠ABO=∠BAO,再求出∠OBC,然后判断出点O是△ABC的外心,根据三角形外心的性质可得OA=OC,再根据等边对等角求出∠OCA=∠OAC,根据翻折的性质可得OF=CF,然后根据等边对等角求出∠COF,再利用三角形的内角和定理和翻折的性质列式计算即可得解.
解答 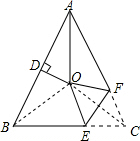 解:如图,连接OB、OC,
解:如图,连接OB、OC,
∵∠BAC=50°,AO为∠BAC的平分线,
∴∠BAO=∠CAO=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×50°=25°,
又∵AB=AC,
∴∠ABC=$\frac{1}{2}$(180°-∠BAC)=$\frac{1}{2}$(180°-50°)=65°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=25°,
∴∠OBC=∠ABC-∠ABO=65°-25°=40°,
∵AO为∠BAC的平分线,AB=AC,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴点O在BC的垂直平分线上,
又∵DO是AB的垂直平分线,
∴点O是△ABC的外心,
∴OA=OC,
∴∠OCA=∠OAC=25°,
根据翻折的性质可得OF=CF,
∴∠COF=∠OCF=25°,
∴∠OFC=130°,
∴∠CFE=65°.
故选C.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形三线合一的性质,等边对等角的性质,以及翻折变换的性质,综合性较强,难度较大,作辅助线,构造出等腰三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
| 次数 | 6 | 12 | 15 | 18 | 20 | 25 | 27 | 30 | 32 | 35 | 36 |
| 人数 | 1 | 2 | 8 | 16 | 10 | 5 | 1 | 2 | 1 | 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差值(千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 8 | 2 | 3 | 2 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| -11+3=-8 | -39+(-21)=-60 | (-2015)+2014=-1 |
| -3-(-1.2)=-1.8 | (-$\frac{3}{4}$)-(+$\frac{1}{4}$)=-1 | (0.04)×(-0.05)=-0.002 |
| (-$\frac{2}{3}$)×(-1$\frac{1}{2}$)=1 | (-32)÷(-8)=4 | (-2$\frac{1}{12}$)÷1.25=-$1\frac{2}{3}$ |
| (-3)4=81 | (-$\frac{1}{2}$3)=-$\frac{1}{8}$ | -$\frac{{2}^{2}}{7}$=-$\frac{4}{7}$. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
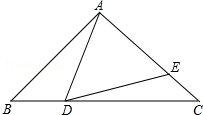 如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com