
 如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.分析 (1)连接OA、OD,如图,根据垂径定理得OD⊥BC,则∠D+∠OFD=90°,再由AC=AF,OA=OD得到∠CAF=∠CFA,∠OAD=∠D,加上∠CFA=∠OFD,所以∠OAD+∠CAF=90°,则OA⊥AC,然后根据切线的判定定理即可得到AC是⊙O切线;
(2)先表示出OD=r,OF=17-r,再在Rt△DOF中利用勾股定理得r2+(17-r)2=132,然后解方程即可得到r的值.
解答 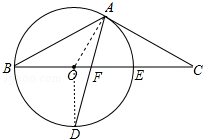 (1)证明:连接OA、OD,如图,
(1)证明:连接OA、OD,如图,
∵D为弧BE的中点,
∴OD⊥BC,
∴∠DOF=90°,
∴∠D+∠OFD=90°,
∵AC=AF,OA=OD,
∴∠CAF=∠CFA,∠OAD=∠D,
而∠CFA=∠OFD,
∴∠OAD+∠CAF=90°,即∠OAC=90°,
∴OA⊥AC,
∴AC是⊙O切线;
(2)解:OD=r,OF=17-r,
在Rt△DOF中,r2+(17-r)2=132,
解得r=5(舍去),r=12;
即⊙O的半径r为12.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了垂径定理.


科目:初中数学 来源: 题型:解答题
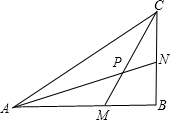 如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连接AN,CM交于P点,求证:∠APM=45°.
如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连接AN,CM交于P点,求证:∠APM=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
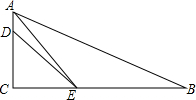 已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE,
已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
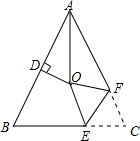 如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )
如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )| A. | 50° | B. | 45° | C. | 65° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | n | B. | 4n+5 | C. | 3n+1 | D. | 3n+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
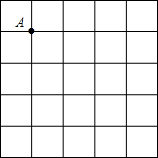 如图,在5×5的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com