
【题目】阅读下面材料:
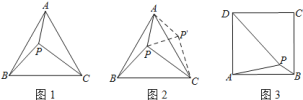
小伟遇到这样一个问题:如图![]() ,在正三角形
,在正三角形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.小伟是这样思考的:如图
的度数.小伟是这样思考的:如图![]() ,利用旋转和全等的知识构造
,利用旋转和全等的知识构造![]() ,连接
,连接![]() ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.
(1)请你回答:图![]() 中
中![]() 的度数等于________.
的度数等于________.
参考小伟同学思考问题的方法,解决下列问题:
(2)如图![]() ,在正方形
,在正方形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数和正方形的边长.
的度数和正方形的边长.
【答案】150°
【解析】
把△APB绕点A逆时针旋转60°得到△![]() ,根据旋转的性质可得P
,根据旋转的性质可得P![]() A=PA,P
A=PA,P![]() C=PB,∠PAP
C=PB,∠PAP![]() =60°,再用勾股定理得出∠P
=60°,再用勾股定理得出∠P![]() PC=90°,然后求出∠AP
PC=90°,然后求出∠AP![]() C,即为∠APB的度数;把
C,即为∠APB的度数;把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,由旋转的性质,
,由旋转的性质,![]() ,
,![]() ,
,![]() ,然后判断出△APP
,然后判断出△APP![]() 是等腰三角形,根据等腰三角形性质求出PP
是等腰三角形,根据等腰三角形性质求出PP![]() ,∠PAP
,∠PAP![]() =45°,再运用勾股定理逆定理得出∠PP
=45°,再运用勾股定理逆定理得出∠PP![]() D=90°,然后求∠AP
D=90°,然后求∠AP![]() D,即为∠APB度数,在求出P
D,即为∠APB度数,在求出P![]() ,P,B三点共线,过点A作AE⊥PP
,P,B三点共线,过点A作AE⊥PP![]() 于E,根据等腰三角的性质求出AE,然后求BE,在直角三角形ABE中,利用勾股定理求出AB即可.
于E,根据等腰三角的性质求出AE,然后求BE,在直角三角形ABE中,利用勾股定理求出AB即可.
(1)![]() .
.
![]() 如图
如图![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
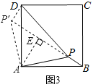
由旋转的性质,![]() ,
,![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,
∵![]() ,
,
∴点![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
过点![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有![]() 个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共
个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共![]() 组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做
组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做![]() 次试验,汇总起来后,摸到红球次数为
次试验,汇总起来后,摸到红球次数为![]() 次.
次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】创意产品蕴含着很多商机,我市某文化创意公司,销售A,B两种创意产品,其中A产品的定价是每件20元,B产品的定价是每件30元.
(1)该公司按定价售出A,B两种产品共600件,若销售总额不低于15000元,则至少销售B产品多少件?
(2)2017年8月,该公司按定价售出A产品300件,B产品400件.2017年9月,公司根据市场情况,适当调整A,B产品的售价,A产品的售价比定价增加了a%,销量与8月保持不变;B产品的售价比定价减少了a%,销量比8月份增加了a%,结果9月份A,B产品的销售总额比8月份增加了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
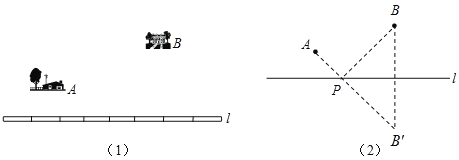
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
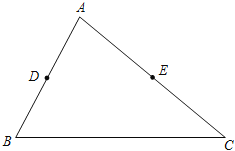
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班学生在颁奖大会上得知该班获得奖励的情况如下表:
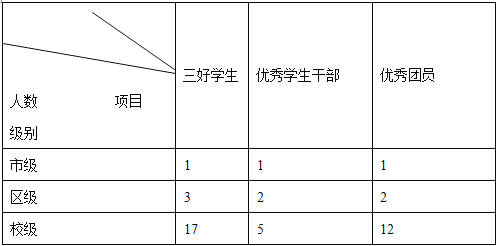
已知该班共有27人获得奖励(每位同学均可获得不同级别、不同类别多项奖励),其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A. 3项 B. 4项 C. 5项 D. 6项
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com