
 如图,在平面直角坐标系中放入一张长方形纸片OABC,其中O是坐标原点,OA,OC分别在x轴,y轴的正半轴上,现在纸片沿CE翻折,使点B落在x轴上,记为B′,若OA=15,OC=9,则折痕CE所在直线的解析式为
如图,在平面直角坐标系中放入一张长方形纸片OABC,其中O是坐标原点,OA,OC分别在x轴,y轴的正半轴上,现在纸片沿CE翻折,使点B落在x轴上,记为B′,若OA=15,OC=9,则折痕CE所在直线的解析式为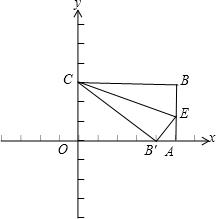 解:∵四边形OABC为正方形,
解:∵四边形OABC为正方形,
|
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACB=90°,且AC=b,BC=a,AB=c,∠A与∠B的平分线交于点O,O到AB的距离为OD.试探究OD与a、b、c的数量关系.
如图,在Rt△ABC中,∠ACB=90°,且AC=b,BC=a,AB=c,∠A与∠B的平分线交于点O,O到AB的距离为OD.试探究OD与a、b、c的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,正方形ABCD的边长为4,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结ED交AC于P,则PB+PE的最小值是
如图,正方形ABCD的边长为4,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结ED交AC于P,则PB+PE的最小值是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是李佳阳和蝴蝶夫人在做数学题时遇到的问题:已知矩形ABCD的顶点A在坐标原点,AB,AD分别在x轴,y轴的正半轴上,点B的坐标为(1,0),点D的坐标为(0,
如图是李佳阳和蝴蝶夫人在做数学题时遇到的问题:已知矩形ABCD的顶点A在坐标原点,AB,AD分别在x轴,y轴的正半轴上,点B的坐标为(1,0),点D的坐标为(0,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知如图,⊙O1与⊙O2外切于点P,过⊙O1上一点B作⊙O1的切线,交⊙O2于点C,D,直线BP交⊙O2于点A.
已知如图,⊙O1与⊙O2外切于点P,过⊙O1上一点B作⊙O1的切线,交⊙O2于点C,D,直线BP交⊙O2于点A.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com