
【题目】(本题14分)已知,在矩形ABCD中,AB=6,BC=8,将矩形ABCD绕着点D按着顺时针方向旋转![]() 得到矩形A/B/C/D,直线DA/、B/C/分别与直线BC相交于点P、Q.
得到矩形A/B/C/D,直线DA/、B/C/分别与直线BC相交于点P、Q.
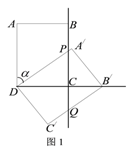
(1)如图1,当矩形A/B/C/D的顶点B/落在射线DC上时,PC的长为_________;
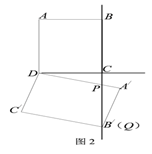
如图2,当矩形A/B/C/D的顶点B/落在射线BC上时,PC的长为_________;
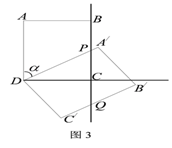
(2)①如图3,当点P位于线段BC上时,求证:DP=PQ.
②在矩形ABCD旋转的过程中(旋转角![]() 满足
满足![]() ),试求出当
),试求出当![]() 时PC的长.
时PC的长.
(3)在矩形ABCD旋转的过程中(旋转角![]() 满足
满足![]() ),以D,B/,P,Q为顶点的四边形能否成为平行四边形?若能,直接写出此时PC的长(或PC的取值范围);若不能,请简要说明理由.
),以D,B/,P,Q为顶点的四边形能否成为平行四边形?若能,直接写出此时PC的长(或PC的取值范围);若不能,请简要说明理由.
【答案】 (1)![]() ;.
;. ![]() ,(2)①证明方法较多.如连结DQ,先证△DCQ≌△DC/Q,再证∠PDQ=∠PQD.等等.②CP=9+
,(2)①证明方法较多.如连结DQ,先证△DCQ≌△DC/Q,再证∠PDQ=∠PQD.等等.②CP=9+![]() 或
或![]() (3)CP=8
(3)CP=8
【解析】:(1)①根据相似三角形的性质得出边的比值即可; ②由全等三角形的判定和性质得出边的关系,再根据勾股定理得出方程解答即可; (2)①由矩形的性质得出线段相等,再利用全等三角形进行判断,利用其性质证明即可; ②根据全等三角形判定和性质得出线段关系,再利用勾股定理得出方程解答即可;
(3)分几种情况进行分析得出以点D,B′,P,Q为顶点的四边形能否成为平行四边形,进而得出CP的值.
解:(1)①∵将矩形ABCD绕点D按顺时针方向旋转,得到矩形A′B′C′D′,AB=6,BC=8,
∴△CDP∽△A′DB′
∴CP=![]() ,
,
同理可得,CP=![]() .
.
(2)①如图所示.
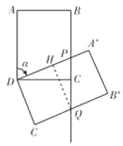
过点Q作QH⊥DA′于H,
则∠QHD=∠HDC′=∠C′=90°,
∴四边形QHDC′为矩形,
∴QH=DC′=DC,
在△DCP和△QHP中,
∵∠QHP=∠DCP=90°×∠QPH=∠DPC×QH=DC,
∴△DCP≌△QHP,
∴DP=PQ.
②当点P在线段BC上时,如图所示,
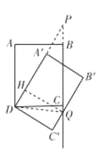
则DP=BP=x,PC=8-x,
在Rt△PCD中,(8-x)2+62=x2,解得x=![]() ,
,
∴PC=BC-BP=8-![]() =
=![]() ,
,
∴矩形ABCD旋转(当0°< ![]() ≤90°时)过程中.
≤90°时)过程中.
当BP=![]() BQ时,CP的长是9+
BQ时,CP的长是9+![]()
![]() 或
或![]() .
.
(3)CP=8.
解法:设矩形DA′B′C′的对角线与直线BC的交点为S.
①当B/在直线BC的右侧时,虽然DP∥B′Q,
但总有DS≥DC>![]() DB′=5,即PQ与B′Q不互相平分,
DB′=5,即PQ与B′Q不互相平分,
以D、B′、P、Q为顶点不能构成平行四边形;
②当B/在直线BC上时,B′、P、Q三点在一条直线上,所以,以D、B′、P、Q为顶点不能构成平行四边形;
③当 B′落在线段AD的延长线上时,如图所示,
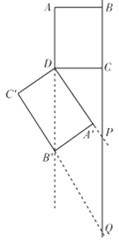
DP∥B′Q,且DB′∥PQ,所以四边形DB′QP为平行四边形,
此时△PCD≌△DA′B,CP=DA′=8;
④当B′在直线BC与直线AD所夹区域时,虽然DP∥B′Q,但DB′与PQ不平行,
所以,以D、B′、P、Q为顶点不能构成平行四边形;
综上,只有B′落在线段AD的延长线上时,四边形DB/QP为平行四边形,此时CP=8.
“点睛”本题考查了矩形的性质,旋转的性质,全等三角形的判定与性质,勾股定理的应用,找出两根三角形的高的关系是本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(﹣2,﹣2)都是“平衡点”.当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )
A.0≤m≤1
B.﹣3≤m≤1
C.﹣3≤m≤3
D.﹣1≤m≤0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)必然事件A的概率为:P(A)=______________.
(2)不可能事件A的概率为:P(A)=______________.
(3)随机事件A的概率为P(A):______________.
(4)随机事件的概率的规律:事件发生的可能性越大,则它的概率越接近于_____________;反之,事件发生的可能性越小,则它的概率越接近于_____________.从1~9这九个自然数中任取一个,是2的倍数的概率是_____________.方程5x=10的解为负数的概率是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师计算学生的学期总评成绩按照如下的标准:平时作业占10%,单元测验占30%,期中考试占25%,期末考试占35%.小丽和小明的成绩如下所示:
学生 | 平时作业 | 单元测验 | 期中考试 | 期未考试 |
小丽 | 80 | 75 | 71 | 88 |
小明 | 76 | 80 | 70 | 90 |
请你通过计算,比较谁的学期总评成绩高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
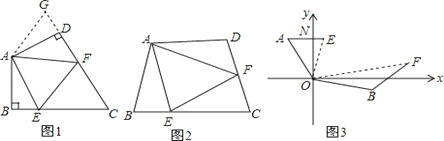
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算错误的是( )
A.a2÷a0a2=a4B.a2÷(a0a2)=1
C.(a+b)2(a+b)3=a5+b5D.(a+b)(a-b)=a2-b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB,AC分别平行于x轴、y轴,若双曲线y=![]() (k≠0)与△ABC有交点,则k的取值范围是____.
(k≠0)与△ABC有交点,则k的取值范围是____.
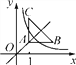
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
(1)如图,已知等腰直角三角形ABC,∠A=90°,试说明:△ABC是生成三角形;
(2)若等腰三角形DEF有一个内角等于36°,请你画出简图说明△DEF是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com