
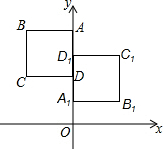
 如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).分析 (1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,据此解答即可.
(2)首先根据A,D的坐标分别是(0,4),(0,2),求出正方形ABCD与正方形A1B1C1D1的边长是多少,然后根据A,D1,D三点的坐标分别是(0,4),(0,3),(0,2),判断出顶点B,C,B1,C1的坐标各是多少即可.
解答 解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4-2=2,
∴B,C的坐标分别是(-2,4),(-2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得
顶点B,C,B1,C1的坐标分别是(-2,4),(-2,2),(2,1),(2,3).
点评 (1)此题主要考查了中心对称的性质和应用,要熟练掌握,解答此题的关键是要明确中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
(2)此题还考查了坐标与图形的性质的应用,要熟练掌握,解答此题的关键是要明确点到坐标轴的距离与这个点的坐标是有区别的,表现在两个方面:①到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关;②距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.


科目:初中数学 来源: 题型:选择题
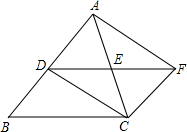 如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 任意四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
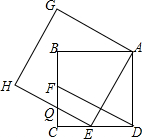 如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.
如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com