练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数（其中a，b，c为常数）的图象如图所示，有以下结论：①；②；③；④关于x的一元二次方程有两个不相等的实数根.其中正确结论的番号是（ ）

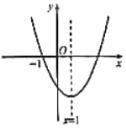
    A.①②④B.①③④C.①④D.③④

    【答案】C

    【解析】

    根据图像，分别判断出a、b、c的符号，即可判断①；根据图像可知：当x＝1时，y＜0，即可判断②；根据抛物线的对称轴为x=1，即可判断③；根据抛物线与x轴的交点个数，即可判断④.

    解：∵抛物线的开口向上

    ∴a＞0

    ∵抛物线的对称轴在y轴右侧

    ∴a、b异号，即b＜0

    ∵抛物线与y轴交于负半轴

    ∴c＜0

    ∴，故①正确；

    由图像可知：当x=1时，y=＜0，故②错误；

    ∵抛物线的对称轴为x=1

    ∴

    整理得：，故③错误；

    ∵抛物线与x轴有两个交点

    ∴关于x的一元二次方程有两个不相等的实数根，故④正确.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，点A（0，4），B（1，m）都在直线y＝﹣2x+b上，反比例函数y＝（x＞0）的图象经过点B．

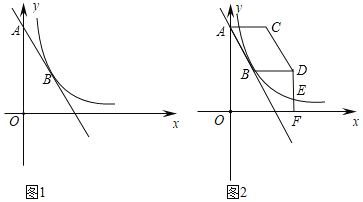
    （1）直接写出m和k的值；

    （2）如图2，将线段AB向右平移n个单位长度（n≥0），得到对应线段CD，连接AC，BD．

    ①在平移过程中，若反比例函数图象与线段AB有交点，求n的取值范围；

    ②在平移过程中，连接BC，若△BCD是直角三角形，请直接写出所有满足条件n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形内接于，，是对角线。点E在的延长线上，且．

    （1）判断与的位置关系，并说明理由；

    （2）与的延长线交于点F，若，，，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标中，直角梯形OABC的边OC、OA分别在x轴、y轴上，AB∥OC，∠AOC=90°，∠BCO=45°，BC=，点C的坐标为（－18，0）.

    （1）求点B的坐标；

    （2）若直线DE交梯形对角线BO于点D，交y轴于点E，且OE=4，OD=2BD，求直线DE的解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．

    （1）求证：△ADE≌△CBF；

    （2）若四边形 BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

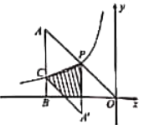
    【题目】如图点P为双曲线上一动点.连接OP并延长到点A，使，过点A作x轴的垂线，垂足为B，交双曲线于点C.当时，连接PC，将沿直线PC进行翻折，则翻折后的与四边形BOPC的重叠部分（图中阴影部分）的面积是_______________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】校园空地上有一面墙，长度为20m，用长为32m的篱笆和这面墙围成一个矩形花圃，如图所示．

    （1）能围成面积是126m2的矩形花圃吗？若能，请举例说明；若不能，请说明理由．

    （2）若篱笆再增加4m，围成的矩形花圃面积能达到170m2吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠B=90°，∠BAC的平分线交BC于点D，以D为圆心，D长为半径作作⊙D.

    ⑴求证：AC是⊙D的切线.

    ⑵设AC与⊙D切于点E，DB=1，连接DE，BF，EF.

    ①当∠BAD= 时，四边形BDEF为菱形；

    ②当AB= 时，△CDE为等腰三角形.

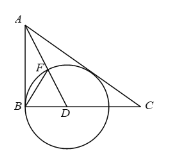
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的切线，切点为B，OA交⊙O于点C，且AC=OC.

    （1）求弧BC的度数；

    （2）设⊙O的半径为5，求图中阴影部分的面积．

    查看答案和解析>>

    同步练习册答案