
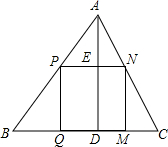
 用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.
用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.分析 解:设△ABC的三条边上的对应高分别为ha,hb,hc,一边分别落在a,b,c上的内接正方形边长分别记为xa,xb,xc,由(1)、(2)可得:$\frac{{x}_{a}}{a}$=$\frac{{h}_{a}-{x}_{a}}{{h}_{a}}$,进而表示出xa=$\frac{a{h}_{a}}{a+{h}_{a}}$,同理xb=$\frac{b{h}_{b}}{b+{h}_{b}}$,xc=$\frac{c{h}_{c}}{c+{h}_{c}}$,然后将它们作差,与0比较,进而得出xa,xb,xc,的大小关系.
解答 解:设△ABC的三条边上的对应高分别为ha,hb,hc.
由(1)、(2)可得:$\frac{{x}_{a}}{a}$=$\frac{{h}_{a}-{x}_{a}}{{h}_{a}}$,
∴xa=$\frac{a{h}_{a}}{a+{h}_{a}}$,
同理xb=$\frac{b{h}_{b}}{b+{h}_{b}}$,xc=$\frac{c{h}_{c}}{c+{h}_{c}}$,
∵xa-xb=$\frac{a{h}_{a}}{a{+h}_{a}}$-$\frac{b{h}_{b}}{b+{h}_{b}}$=$\frac{2s}{a+{h}_{a}}$-$\frac{2s}{\;}$b+hb=2S($\frac{1}{a+{h}_{a}}$-$\frac{1}{b+{h}_{b}}$),
=$\frac{2s}{(a+{h}_{a})(b+{h}_{b})}$(b+hb-a-ha),
=$\frac{2s}{(a+{h}_{a})(b+{h}_{b})}$(b-a)(1-$\frac{{h}_{a}}{b}$),
∵a>b,ha<b,
∴(b-a)(1-$\frac{{h}_{a}}{b}$)<0,
即xa-xb<0,
∴xa<xb,
同理:xb<xc,
∴xa<xb<xc.
∴乙同学说的正确.
点评 本题主要考查了相似三角形的判定与性质,熟练掌握相似三角形的对应高的比等于相似比的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
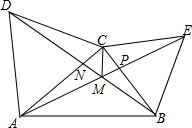 还记得在全等三角形中证明的一个习题吗?如图所示,已知在△ABC中,分别以AC、BC为边,向外作正△ACD、正△BCE,BD与AE相交于M,求证:AE=BD
还记得在全等三角形中证明的一个习题吗?如图所示,已知在△ABC中,分别以AC、BC为边,向外作正△ACD、正△BCE,BD与AE相交于M,求证:AE=BD查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2x2-4x+3=0 | B. | 2x2+4x-3=0 | C. | 2x2-4x+3=0 | D. | 2x2-4x-3=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
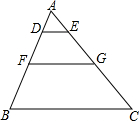 如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.
如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com