
分析 (1)设每千克樱桃应降价x元,利用销售量×每件利润=2240元列出方程求解即可;
(2)为了让利于顾客因此应下降6元,求出此时的销售单价即可确定几折.
解答 (1)解:设每千克樱桃应降价x元,
根据题意,得:(60-x-40)(100+$\frac{x}{3}$×30)=2240,
解得:x1=4,x2=6,
答:每千克樱桃应降价4元或6元;
(2)由(1)可知每千克樱桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克樱桃应降价6元.
此时,售价为:60-6=54(元),
$\frac{54}{60}$×100%=90%.
故答案是:9.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
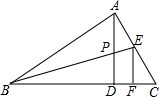 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,P是AD的中点,BP交AC于点E,EF⊥BC于点F,若AE=3,EC=4,求EF的值.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,P是AD的中点,BP交AC于点E,EF⊥BC于点F,若AE=3,EC=4,求EF的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
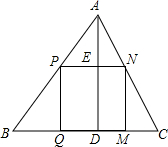 用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.
用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
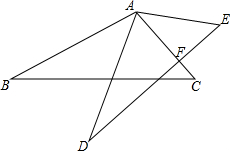 在讲完全等三角形后,数学老师王老师布置了一道数学题:如图所示,已知△ABC≌△ADE,其中∠CAE=40°,∠C=50°,则DE与AC有何位置关系?请说明理由.
在讲完全等三角形后,数学老师王老师布置了一道数学题:如图所示,已知△ABC≌△ADE,其中∠CAE=40°,∠C=50°,则DE与AC有何位置关系?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com