【题目】2002年国际数学家大会在北京召开，大会选用了赵爽弦图作为会标的中心图案．如图，由四个全等的直角三角形与一个小正方形拼成一个大正方形．如果大正方形的面积是25，直角三角形较长的直角边长是a，较短的直角边长是b，且（a+b）2的值为49，那么小正方形的面积是（ ）
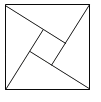
A.2B.0.5C.13D.1
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】如图，小颖在教学楼四层楼上，每层楼高均为3米，测得目高1.5米，看到校园里的圆形花园最近点的俯角为60°，最远点的俯角为30°，请你帮小颖算出圆形花园的面积是多少平方米？（结果保留1位小数）
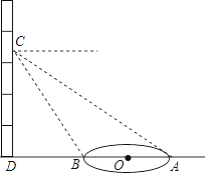
查看答案和解析>>
科目：初中数学 来源： 题型：
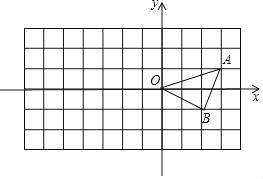
【题目】方格纸中每个小正方形的边长都是单位1，△OAB在平面直角坐标系中的位置如图所示．解答问题：
（1）请按要求对△ABO作如下变换：
①将△OAB向下平移2个单位，再向左平移3个单位得到△O1A1B1；
②以点O为位似中心，位似比为2：1，将△ABC在位似中心的异侧进行放大得到△OA2B2．
（2）写出点A1，A2的坐标： ， ；
（3）△OA2B2的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
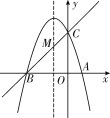
【题目】如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－1，且经过A(1,0)，C(0，3)两点，与x轴的另一个交点为B.
(1)若直线y＝mx＋n经过B，C两点，求直线BC和抛物线的解析式；
(2)在抛物线的对称轴x＝－1 上找一点M，使点M到点A的距离与到点C的距离之和最小，求点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），在
和
中，
为边
上一点，
平分
，
，
.
（1）求证：
（2）如图（2），若
，连接
交于
，
为边
上一点，满足
，连接
交于
. ①求
的度数；
②若
平分
，试说明：平分
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在规格为8×8的边长为1个单位的正方形网格中（每个小正方形的边长为1），△ABC的三个顶点都在格点上，且直线m、n互相垂直．
（1）画出△ABC关于直线n的对称图形△A′B′C′；
（2）直线m上存在一点P，使△APB的周长最小；
①在直线m上作出该点P；（保留画图痕迹）
②△APB的周长的最小值为 ．（直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，-1）．
（1）请以y轴为对称轴，画出与△ABC对称的△A1B1C1，并直接写出点A1、B1、C1的坐标；
（2）△ABC的面积是 ．
（3）点P（a+1，b-1）与点C关于x轴对称，则a= ，b= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，图形的运动只改变图形的位置，不改变图形的形状、大小，运动前后的两个图形全等，翻折就是这样．如图1，将△ABC沿AD翻折，使点C落在AB边上的点C'处，则△ADC≌△ADC'．
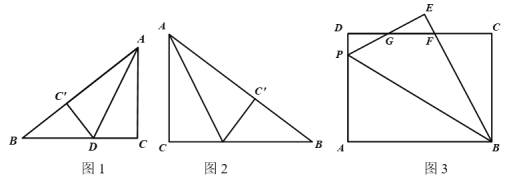
尝试解决：（1）如图2，△ABC中，∠C=90°，AC=6，BC=8，将△ABC沿AD翻折，使点C落在AB边上的点C'处，求CD的长．
（2）如图3，在长方形ABCD中，AB=8，AD=6，点P在边AD上，连接BP，将△ABP沿BP翻折，使点A落在点E处，PE、BE分别与CD交于点G、F，且DG=EG．
①求证：PE=DF；
②求AP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】五一期间，某商场计划购进甲、乙两种商品，已知购进甲商品1件和乙商品3件共需240元；购进甲商品2件和乙商品1件共需130元．
（1）求甲、乙两种商品每件的进价分别是多少元？
（2）商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
