
【题目】如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC∶CA=4∶3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点
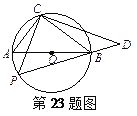
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求这个最大面积S.
【答案】(1)略
(2)![]()
(3)![]()
【解析】
解:(1)∵AB为直径,∴∠ACB=90°.又∵PC⊥CD,∴∠PCD=90°.
而∠CAB=∠CPD,∴△ABC∽△PCD.∴![]() .
.
∴AC·CD=PC·BC;
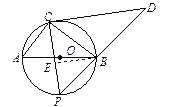
(2)当点P运动到AB弧中点时,过点B作BE⊥PC于点E.
∵P是AB中点,∴∠PCB=45°,CE=BE=![]() BC=2
BC=2![]() .
.
又∠CAB=∠CPB,∴tan∠CPB=tan∠CAB=![]() .∴PE=
.∴PE=![]() =
=![]() =
=![]() .
.
从而PC=PE+EC=![]() .由(1)得CD=
.由(1)得CD=![]() PC=
PC=![]()
(3)当点P在AB上运动时,S△PCD=![]() PC·CD.由(1)可知,CD=
PC·CD.由(1)可知,CD=![]() PC.
PC.
∴S△PCD=![]() PC2.故PC最大时,S△PCD取得最大值;
PC2.故PC最大时,S△PCD取得最大值;
而PC为直径时最大,∴S△PCD的最大值S=![]() ×52=
×52=![]() .
.


科目:初中数学 来源: 题型:
【题目】今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量![]() (千克)与销售价
(千克)与销售价![]() (元/千克)之间的函数关系如图所示:
(元/千克)之间的函数关系如图所示:
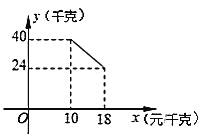
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
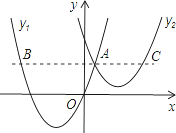
【题目】如图,抛物线y1=a(x+2)2-3与y2=![]() (x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是( )
(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是( )
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一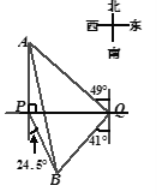 知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
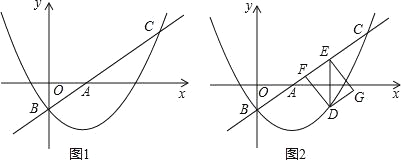
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
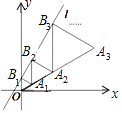
【题目】如图,在平面直角坐标系中,直线l:y=![]() 与y轴交于点B1,以OB1为一边在OB1右侧作等边三角形A1OB1,过点A1作A1B2平行于y轴,交直线l于点B2,以A1B2为一边在A1B2右侧作等边三角形A2A1B2,过点A2作A2B3平行于y轴,交直线l于点B3,以A2B3为一边在A2B3右侧作等边三角形A3A2B3,……则点A2019的纵坐标是( )
与y轴交于点B1,以OB1为一边在OB1右侧作等边三角形A1OB1,过点A1作A1B2平行于y轴,交直线l于点B2,以A1B2为一边在A1B2右侧作等边三角形A2A1B2,过点A2作A2B3平行于y轴,交直线l于点B3,以A2B3为一边在A2B3右侧作等边三角形A3A2B3,……则点A2019的纵坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E. F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
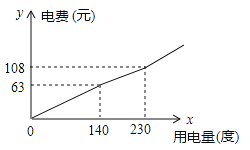
【题目】为了倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式。
(1)根据图象,阶梯电价方案分为三个档次,填写下表:

(2)求每月用电量为100度时所需交的电费:
(3)第二档每用电费y(元)与用电量(度)间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电310度,交电费168元,求m的值
查看答案和解析>>
科目:初中数学 来源: 题型:
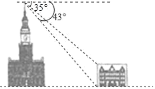
【题目】如图,甲、乙两座建筑物的水平距离BC为30m,从甲的顶部A处测得乙的顶部D处的俯角为35°测得底部C处的俯角为43°,求甲、乙两建筑物的高度AB和DC(结果取整数).
(参考数据:tan35°≈0.70,tan43°≈0.93)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com